
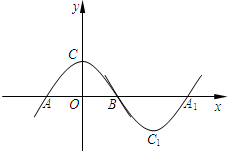
 (2012•静海县二模)如图,抛物线m:y=ax2+b(a<0,b>0)与x轴于点A、B(点A在点B的左侧),与y轴交于点C.将抛物线m绕点B旋转180°,得到新的抛物线n,它的顶点为C1,与x轴的另一个交点为A1.若四边形AC1A1C为矩形,则a,b应满足的关系式为( )
(2012•静海县二模)如图,抛物线m:y=ax2+b(a<0,b>0)与x轴于点A、B(点A在点B的左侧),与y轴交于点C.将抛物线m绕点B旋转180°,得到新的抛物线n,它的顶点为C1,与x轴的另一个交点为A1.若四边形AC1A1C为矩形,则a,b应满足的关系式为( )-
|
-
|
-
|
-
|
| OC2+OB2 |
b2-
|
-
|
b2-
|
| b |
| a |
| b |
| a |


科目:初中数学 来源: 题型:
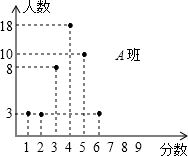 (2012•静海县二模)现有A、B两个班级,每个班级各有45名学生参加一次测验,每名参加者可获得0、1、2、3、4、5、6、7、8、9分这几种不同分值中的一种.测试结果A班的成绩如下图所示,B班的成绩如表所示.
(2012•静海县二模)现有A、B两个班级,每个班级各有45名学生参加一次测验,每名参加者可获得0、1、2、3、4、5、6、7、8、9分这几种不同分值中的一种.测试结果A班的成绩如下图所示,B班的成绩如表所示.| 分数 | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
| 人数 | 1 | 3 | 5 | 7 | 6 | 8 | 6 | 4 | 3 | 2 |
查看答案和解析>>
科目:初中数学 来源: 题型:
| 16 |
| 3 |
| 16 |
| 3 |
| 88 |
| 9 |
| 88 |
| 9 |
查看答案和解析>>
科目:初中数学 来源: 题型:

查看答案和解析>>
科目:初中数学 来源: 题型:
| 3 |
| 2 |
| k |
| x |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com