
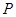 与点
与点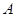 重合(此时AC=PN+CN);当伞慢慢撑开时,动点
重合(此时AC=PN+CN);当伞慢慢撑开时,动点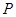 由
由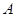 向
向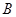 移动;当点
移动;当点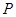 到过点
到过点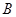 时,伞张得最开.已知伞在撑开的过程中,总有
时,伞张得最开.已知伞在撑开的过程中,总有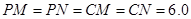 分米,
分米,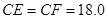 分米,
分米,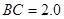 分米
分米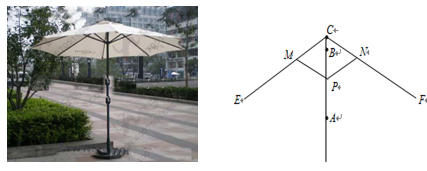
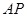 长的取值范围; (2)当
长的取值范围; (2)当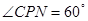 时,求
时,求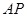 的值;
的值;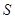 (结果保留
(结果保留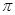 ).
).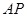 ≤10. (2)6(3)
≤10. (2)6(3)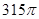

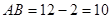
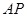 的取值范围为:0≤
的取值范围为:0≤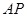 ≤10. ····················· 1分
≤10. ····················· 1分 ∴
∴ 等边三角形. ∴
等边三角形. ∴ .
. .
.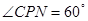 时,
时, 分米. ······················ 2分
分米. ······················ 2分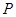 与点
与点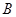 重合.
重合. 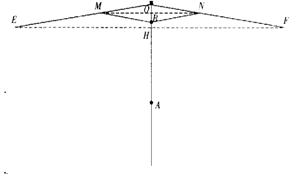
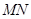 ,
, .分别交
.分别交 于
于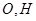
 ,
,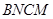 菱形,
菱形,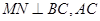 是
是 的平分线,
的平分线,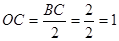 .
.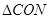 中
中 .
. ,
, 是
是 的平分线,
的平分线, .
.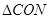 ~
~ .
.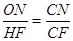 .∴
.∴ 。
。 .
.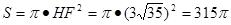 (平方分米). ·············· 5分
(平方分米). ·············· 5分

 学而优暑期衔接南京大学出版社系列答案
学而优暑期衔接南京大学出版社系列答案 Happy holiday欢乐假期暑假作业广东人民出版社系列答案
Happy holiday欢乐假期暑假作业广东人民出版社系列答案 快乐暑假暑假能力自测中西书局系列答案
快乐暑假暑假能力自测中西书局系列答案科目:初中数学 来源:不详 题型:解答题
 轴上的一个动点,M是线段AC的中点.把线段AM进行以A为旋转中心、向顺时针方向旋转90°的旋转变换得到AB.过B作
轴上的一个动点,M是线段AC的中点.把线段AM进行以A为旋转中心、向顺时针方向旋转90°的旋转变换得到AB.过B作 轴的垂线、过点C作
轴的垂线、过点C作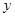 轴的垂线,两直线交于点D,直线DB交
轴的垂线,两直线交于点D,直线DB交 轴于一点E.
轴于一点E.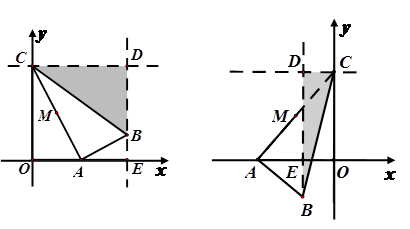
 ,
, =3,则点B的坐标为 ▲ ,若
=3,则点B的坐标为 ▲ ,若 =-3,,则点B的坐标为 ▲ ;
=-3,,则点B的坐标为 ▲ ; >0,△BCD的面积为
>0,△BCD的面积为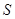 ,则
,则 为何值时,
为何值时,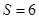 ?
? ,使得以B、C、D为顶点的三角形与△AOC相似?若存在,求此时
,使得以B、C、D为顶点的三角形与△AOC相似?若存在,求此时 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
 的边长为
的边长为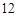 ,
,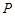 为边
为边 延长线上的一点,
延长线上的一点,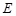 为
为 的中点,
的中点, 的垂直平分线交边
的垂直平分线交边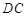 于
于 ,交边
,交边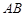 的延长线于
的延长线于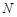 .当
.当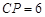 时,
时,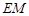 与
与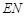 的比值是多少?
的比值是多少?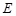 作直线平行于
作直线平行于 交
交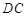 ,
,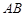 分别于
分别于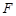 ,
,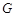 ,如图
,如图 ,则可得:
,则可得: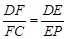 ,因为
,因为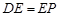 ,所以
,所以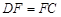 .可求出
.可求出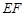 和
和 的值,进而可求得
的值,进而可求得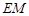 与
与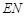 的比值.
的比值.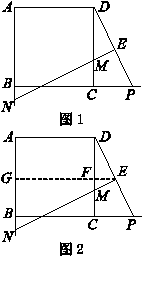
 的结论.你认为小东的这个结论正确吗?如果正确,请给予证明;如果不正确,请说明理由.
的结论.你认为小东的这个结论正确吗?如果正确,请给予证明;如果不正确,请说明理由.查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
 ,AC=
,AC= ,BC=6.
,BC=6.
查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
 ;(4分)
;(4分) 的面积S. (2分)
的面积S. (2分)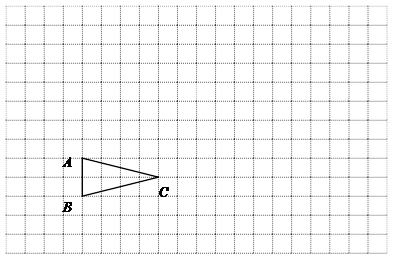
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com