
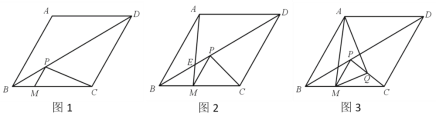
ЁОЬтФПЁПвбжЊСтаЮABCDжаЃЌЁЯABC=60ЁуЃЌAB=4ЃЌЕуMдкBCБпЩЯЃЌЙ§ЕуMзїPMЁЮABНЛЖдНЧЯпBDгкЕуPЃЌСЌНгPCЃЎ
ЃЈ1ЃЉШчЭМ1ЃЌЕБBM=1ЪБЃЌЧѓPCЕФГЄЃЛ
ЃЈ2ЃЉШчЭМ2ЃЌЩшAMгыBDНЛгкЕуEЃЌЕБЁЯPCM=45ЁуЪБЃЌЧѓжЄЃК![]() =
=![]() ЃЛ
ЃЛ
ЃЈ3ЃЉШчЭМ3ЃЌШЁPCЕФжаЕуQЃЌСЌНгMQЃЌAQЃЎ
ЂйЧыЬНОПAQКЭMQжЎМфЕФЪ§СПЙиЯЕЃЌВЂаДГіЬНОПЙ§ГЬЃЛ
ЂкЁїAMQЕФУцЛ§газюаЁжЕТ№ЃПШчЙћгаЃЌЧыжБНгаДГіетИізюаЁжЕЃЛШчЙћУЛгаЃЌЧыЫЕУїРэгЩЃЎ
ЁОД№АИЁПЃЈ1ЃЉ![]() ЃЛЃЈ2ЃЉМћНтЮіЃЛЃЈ3ЃЉЂйAQ=
ЃЛЃЈ2ЃЉМћНтЮіЃЛЃЈ3ЃЉЂйAQ=![]() MQЃЌМћНтЮіЃЌЂкгаЃЌ
MQЃЌМћНтЮіЃЌЂкгаЃЌ![]()
ЁОНтЮіЁП
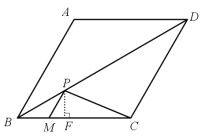
ЃЈ1ЃЉЙ§ЕуPзїPFЁЭBCгкЕуFЃЌЪзЯШРћгУСтаЮЕФаджЪЕУГіЁЯABD=ЁЯCBD=30ЁуЃЌAB=BC=CD=AD=4ЃЌШЛКѓИљОнЦНааЯпЕФаджЪЕУГіЁЯABD=ЁЯBPM=ЁЯCBD=30ЁуЃЌЁЯPMF =ЁЯABC=60ЁуЃЌНјЖјПЩЧѓГіPM,PF,MFЕФГЄЖШЃЌДгЖјFCЕФГЄЖШПЩЧѓЃЌзюКѓРћгУЙДЙЩЖЈРэМДПЩЧѓPCЕФГЄЖШЃЛ
ЃЈ2ЃЉЙ§ЕуPзїPGЁЭBCгкЕуGЃЌЩшMG=xЃЌгЩЃЈ1ЃЉПЩжЊЃКBM=PM=2xЃЌGC=PG=![]() xЃЌШЛКѓРћгУBM+MG+GC=BCЧѓГіxЕФжЕЃЌНјЖјПЩЧѓГіBMЕФГЄЖШЃЌзюКѓРћгУЦНааЯпЗжЯпЖЮГЩБШР§МДПЩЕУГіНсТлЃЛ
xЃЌШЛКѓРћгУBM+MG+GC=BCЧѓГіxЕФжЕЃЌНјЖјПЩЧѓГіBMЕФГЄЖШЃЌзюКѓРћгУЦНааЯпЗжЯпЖЮГЩБШР§МДПЩЕУГіНсТлЃЛ
ЃЈ3ЃЉЂйбгГЄMQгыCDНЛгкЕуHЃЌСЌНгAH,ACЃЌЪзЯШжЄУїЁїPMQЁеЁїCHQЃЌдђгаPM=CH=BMЃЌMQ=HQЃЌШЛКѓРћгУСтаЮЕФаджЪКЭЕШБпШ§НЧаЮЕФаджЪжЄУї ЁїABMЁеЁїACHЃЌдђгаAM=AHЃЌЁЯBAM=ЁЯCAHЃЌдђЁїAMHЮЊЕШБпШ§НЧаЮЃЌдђРћгУЕШБпШ§НЧаЮЕФаджЪМДПЩЕУГіAQ,MQжЎМфЕФЙиЯЕЃЛ
ЂкИљОнЂйжаЕФНсТлга![]() ЃЌЕБAMШЁзюаЁжЕЪБЃЌMQгазюаЁжЕЃЌЕБ
ЃЌЕБAMШЁзюаЁжЕЪБЃЌMQгазюаЁжЕЃЌЕБ![]() ЪБЃЌAMзюаЁЃЌЧѓГіДЫЪБЕФAM,MQЕФжЕЃЌзюКѓРћгУ
ЪБЃЌAMзюаЁЃЌЧѓГіДЫЪБЕФAM,MQЕФжЕЃЌзюКѓРћгУ![]() ЧѓНтМДПЩЃЎ
ЧѓНтМДПЩЃЎ
НтЃКЃЈ1ЃЉШчЭМЃЌЙ§ЕуPзїPFЁЭBCгкЕуFЃЎ
ЁпЫФБпаЮABCDЪЧСтаЮЃЌЁЯABC=60ЁуЃЌ
ЁрЁЯABD=ЁЯCBD=30ЁуЃЌAB=BC=CD=AD=4ЃЎ
ЁпPMЁЮABЃЌ
ЁрЁЯABD=ЁЯBPM=ЁЯCBD=30ЁуЃЌЁЯPMF =ЁЯABC=60ЁуЃЌ
ЁрPM=BM=1ЃЌ
ЁрMF=![]() PM=
PM=![]() ЃЌPF=
ЃЌPF=![]() ЃЌ
ЃЌ
ЁрFC=BC-BM-MF=4-1-![]() =
=![]() ЃЌ
ЃЌ
ЁрPC=![]() =
=![]() ЃЎ
ЃЎ
ЃЈ2ЃЉжЄУїЃКШчЭМЃЌЙ§ЕуPзїPGЁЭBCгкЕуGЃЎ
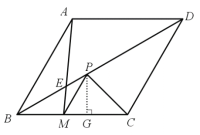
ЁпЁЯPCM=45ЁуЃЌ
ЁрЁЯCPG=ЁЯPCM=45ЁуЃЌ
ЁрPG=GCЃЎ
ЩшMG=xЃЌгЩЃЈ1ЃЉПЩжЊЃКBM=PM=2xЃЌGC=PG=![]() xЃЌ
xЃЌ
гЩBM+MG+GC=BCЕУЃК2x+x+![]() x=4ЃЌ
x=4ЃЌ
Ёрx=![]() ЃЌ
ЃЌ
ЁрBM=![]() ЃЎ
ЃЎ
ЁпЫФБпаЮABCDЪЧСтаЮЃЌ
ЁрBMЁЮADЃЌ
Ёр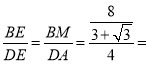
![]()
ЃЈ3ЃЉЂйШчЭМЃЌбгГЄMQгыCDНЛгкЕуHЃЌСЌНгAH,ACЃЎ
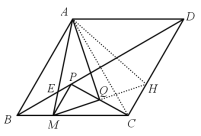
ЁпPMЁЮABЁЮCDЃЌ
ЁрЁЯPMQ=ЁЯCHQЃЌЁЯMPQ=ЁЯHCQЃЎ
ЁпQЪЧPCЕФжаЕуЃЌ
ЁрPQ=CQЃЌ
ЁрЁїPMQЁеЁїCHQЃЌ
ЁрPM=CH=BMЃЌMQ=HQЃЎ
ЁпЫФБпаЮABCDЪЧСтаЮЃЌЁЯABC=60ЁуЃЌ
ЁрЁїABCЮЊЕШБпШ§НЧаЮЃЌ
ЁрAB=ACЃЌЁЯABM=ЁЯACH=60ЁуЃЌ
ЁрЁїABMЁеЁїACHЃЌ
ЁрAM=AHЃЌЁЯBAM=ЁЯCAHЃЌ
ЁрЁЯMAH=ЁЯBAC=60ЁуЃЌ
ЁрЁїAMHЮЊЕШБпШ§НЧаЮЃЌ
ЁрAQЁЭMHЃЌЁЯMAQ=![]() ЁЯMAH=30ЁуЃЌ
ЁЯMAH=30ЁуЃЌ
ЁрAQ=![]() MQЃЎ
MQЃЎ
ЂкЁпAQЁЭMHЃЌЁЯMAQ=![]() ЁЯMAH=30ЁуЃЌ
ЁЯMAH=30ЁуЃЌ
![]() ЃЌ
ЃЌ
ЁрЕБAMШЁзюаЁжЕЪБЃЌMQгазюаЁжЕЃЎ
ЕБ![]() ЪБЃЌAMзюаЁЃЌДЫЪБ
ЪБЃЌAMзюаЁЃЌДЫЪБ![]() ЃЌ
ЃЌ
ЁрMQЕФзюаЁжЕЮЊ![]() ЃЌ
ЃЌ
ДЫЪБ![]()
ЁрЁїAMQЕФУцЛ§газюаЁжЕЃЌзюаЁжЕЮЊ![]()


 бЇСЗПьГЕЕРПьРжМйЦкКЎМйзївЕЯЕСаД№АИ
бЇСЗПьГЕЕРПьРжМйЦкКЎМйзївЕЯЕСаД№АИ
| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЖЈвхЃКНЋКЏЪ§lЕФЭМЯѓШЦЕуPЃЈmЃЌ0ЃЉа§зЊ180ЁуЃЌЕУЕНаТЕФКЏЪ§l'ЕФЭМЯѓЃЌЮвУЧГЦКЏЪ§l'ЪЧКЏЪ§ЙигкЕуPЕФЯрЙиКЏЪ§ЃЎ
Р§ШчЃКЕБmЃН1ЪБЃЌКЏЪ§yЃНЃЈx+1ЃЉ2+5ЙигкЕуPЃЈ1ЃЌ0ЃЉЕФЯрЙиКЏЪ§ЮЊyЃНЉЃЈxЉ3ЃЉ2Љ5ЃЎ
ЃЈ1ЃЉЕБmЃН0ЪБ
ЂйвЛДЮКЏЪ§yЃНxЉ1ЙигкЕуPЕФЯрЙиКЏЪ§ЮЊ ЃЛ
ЂкЕуЃЈ![]() ЃЌЉ
ЃЌЉ![]() ЃЉдкЖўДЮКЏЪ§yЃНЉax2Љax+1ЃЈaЁй0ЃЉЙигкЕуPЕФЯрЙиКЏЪ§ЕФЭМЯѓЩЯЃЌЧѓaЕФжЕЃЎ
ЃЉдкЖўДЮКЏЪ§yЃНЉax2Љax+1ЃЈaЁй0ЃЉЙигкЕуPЕФЯрЙиКЏЪ§ЕФЭМЯѓЩЯЃЌЧѓaЕФжЕЃЎ
ЃЈ2ЃЉКЏЪ§yЃНЃЈxЉ1ЃЉ2+2ЙигкЕуPЕФЯрЙиКЏЪ§yЃНЉЃЈx+3ЃЉ2Љ2ЃЌдђmЃНЁЁ ЁЁЃЛ
ЃЈ3ЃЉЕБmЉ1ЁмxЁмm+2ЪБЃЌКЏЪ§yЃНx2ЉmxЉ![]() m2ЙигкЕуPЃЈmЃЌ0ЃЉЕФЯрЙиКЏЪ§ЕФзюДѓжЕЮЊ6ЃЌЧѓmЕФжЕЃЎ
m2ЙигкЕуPЃЈmЃЌ0ЃЉЕФЯрЙиКЏЪ§ЕФзюДѓжЕЮЊ6ЃЌЧѓmЕФжЕЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌдкБпГЄЖМЪЧ1ЕФаЁе§ЗНаЮзщГЩЕФЭјИёжаЃЌ![]() ОљЮЊИёЕуЃЌЯпЖЮ
ОљЮЊИёЕуЃЌЯпЖЮ![]() ЃЌ
ЃЌ![]() ЯрНЛгкЕу
ЯрНЛгкЕу![]() .
.

ЃЈ1ЃЉ![]() ________ЃЛ
________ЃЛ
ЃЈ2ЃЉЩш![]() ЃЌНЋЯпЖЮ
ЃЌНЋЯпЖЮ![]() ШЦЕу
ШЦЕу![]() ФцЪБеыа§зЊ
ФцЪБеыа§зЊ![]() ЕФНЧЃЌЕу
ЕФНЧЃЌЕу![]() ЕФЖдгІЕуЮЊ
ЕФЖдгІЕуЮЊ![]() ЃЌЧыФуНшжњЭјИёЃЌЪЙгУЮоПЬЖШЕФжБГпЛГіЕу
ЃЌЧыФуНшжњЭјИёЃЌЪЙгУЮоПЬЖШЕФжБГпЛГіЕу![]() ЃЌВЂМђвЊЫЕУїФуЪЧдѕУДЛЕФ___________.
ЃЌВЂМђвЊЫЕУїФуЪЧдѕУДЛЕФ___________.
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЁЖОХеТЫуЪѕЁЗРягавЛЕРжјУћЫуЬтЃКЁАНёгаЩЯКЬШ§БќЃЌвцЪЕСљЖЗЃЌЕБЯТКЬЪЎБќЃЎЯТКЬЮхБќЃЌвцЪЕвЛЖЗЃЌЕБЩЯКЬЖўГЫЁЂЮЪЩЯЁЂЯТКЬЪЕвЛГЫИїМИКЮЃПЁБДѓвтЪЧЃК3РІЩЯЕШЙШзгНсГіЕФСИЪГЃЌдйМгЃЎЩЯСљЖЗЃЌЯрЕБгк10РІЯТЕШЙШзгНсГіЕФСИЪГЃЎ5РІЯТЕШЙШзгНсГіЕФСИЪГЃЌдйМгЩЯвЛЖЗЃЌЯрЕБгк2РІЩЯЕШЙШзгНсГіЕФСИЪГЃЎЮЪЃКЩЯЕШЙШзгКЭЯТЕШЙШзгУПРІФмНсГіЖрЩйЖЗСИЪГЃПЧыНтД№ЩЯЪіЮЪЬтЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
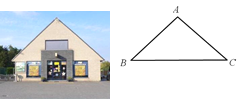
ЁОЬтФПЁПЕШбќШ§НЧаЮЕФЮнЖЅЃЌЪЧНЈжўжаОГЃВЩгУЕФНсЙЙаЮЪНЃЎдкШчЭМЫљЪОЕФЕШбќШ§НЧаЮЮнЖЅABCжаЃЌAB=ACЃЌВтЕУBC=20УзЃЌЁЯC=41ЁуЃЌЧѓЖЅЕуAЕНBCБпЕФОрРыЪЧЖрЩйУзЃПЃЈНсЙћОЋШЗЕН0.1УзЃЎВЮПМЪ§ОнЃКsin41ЁуЁж0.656ЃЌcos41ЁуЁж0.755ЃЌtan41ЁуЁж0.869ЃЎЃЉ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌе§ЗНаЮ![]() ЕФБп
ЕФБп![]() дке§ЗНаЮ
дке§ЗНаЮ![]() ЕФБп
ЕФБп![]() ЩЯЃЌСЌНс
ЩЯЃЌСЌНс![]() ЁЂ
ЁЂ![]() ЃЎ
ЃЎ
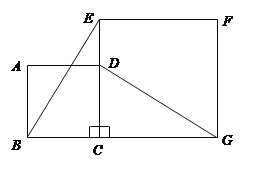
ЃЈ1ЃЉЙлВьВТЯы![]() гы
гы![]() жЎМфЕФДѓаЁЙиЯЕЃЌВЂжЄУїФуЕФНсТлЃЛ
жЎМфЕФДѓаЁЙиЯЕЃЌВЂжЄУїФуЕФНсТлЃЛ
ЃЈ2ЃЉЭМжаЪЧЗёДцдкЭЈЙ§а§зЊФмЙЛЛЅЯржиКЯЕФСНИіШ§НЧаЮЃПШєДцдкЃЌЫЕГіа§зЊЙ§ГЬЃЛШєВЛДцдкЃЌЧыЫЕУїРэгЩЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
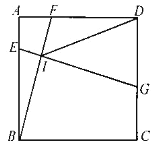
ЁОЬтФПЁПШчЭМЃЌдкБпГЄЮЊ6ЕФе§ЗНаЮABCDжаЃЌЕуEЁЂFЁЂGЗжБ№дкБпABЁЂADЁЂCDЩЯЃЌEGгыBFНЛгкЕуIЃЌAE=2ЃЌBF=EGЃЌDG>AEЃЌдђDIЕФзюаЁжЕЮЊ________.
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌвЛСаПьГЕДгМзЕиЪЛЭљввЕиЃЌвЛСаТ§ГЕДгввЕиЪЛЭљМзЕиЃЌСНГЕЭЌЪБГіЗЂЃЌЩшТ§ГЕааЪЛЕФЪБМфЮЊ![]() СНГЕжЎМфЕФОрРыЮЊ
СНГЕжЎМфЕФОрРыЮЊ![]() ЃЌЭМжаЕФелЯпБэЪО
ЃЌЭМжаЕФелЯпБэЪО![]() гы
гы![]() жЎМфЕФКЏЪ§ЙиЯЕЃЌЯТСаЫЕЗЈжаДэЮѓЕФЪЧЃЈ ЃЉ
жЎМфЕФКЏЪ§ЙиЯЕЃЌЯТСаЫЕЗЈжаДэЮѓЕФЪЧЃЈ ЃЉ
A.МзввСНЕиЯрОр![]() B.Еу
B.Еу![]() БэЪОДЫЪБСНГЕЯргі
БэЪОДЫЪБСНГЕЯргі
C.Т§ГЕЕФЫйЖШЮЊ![]() D.елЯп
D.елЯп![]() БэЪОТ§ГЕЯШМгЫйКѓМѕЫйзюКѓЕНДяМзЕи
БэЪОТ§ГЕЯШМгЫйКѓМѕЫйзюКѓЕНДяМзЕи
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
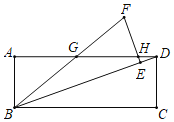
ЁОЬтФПЁПШчЭМЃЌОиаЮABCDжаЃЌНЋЁїBCDШЦЕуBФцЪБеыа§зЊЕУЁїBEFЃЌЦфжаЕуCЕФЖдгІЕуEЧЁКУТфдкBDЩЯЃЎBFЃЌEFЗжБ№НЛБпADгкЕуGЃЌHЃЎШєGHЃН4HDЃЌдђcosЁЯDBCЕФжЕЮЊ_____ЃЎ
ВщПДД№АИКЭНтЮі>>
АйЖШжТаХ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com