
【题目】如图,已知△ABC是等边三角形,D、E分别在边BC、AC上,且CD=CE,连接DE并延长至点F,使EF=AE,连接AF、BE和CF.
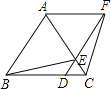
(1)请在图中找出一对全等三角形,用符号“≌”表示,并加以证明;
(2)判断四边形ABDF是怎样的四边形,并说明理由;
(3)若AB=6,BD=2DC,求四边形ABEF的面积..
【答案】(1)见解析;(2)平行四边形;(3)![]()
【解析】试题分析:(1)从图上及已知条件容易看出△BDE≌△FEC,△BCE≌△FDC,△ABE≌△ACF.判定两个三角形全等时,必须有边的参与,所以此题的关键是找出相等的边.
(2)由(1)的结论容易证明AB∥DF,BD∥AF,两组对边分别平行的四边形是平行四边形.
(3)EF∥AB,EF≠AB,四边形ABEF是梯形,只要求出此梯形的面积即可.
试题解析:解:(1)△BDE≌△FEC或△BCE≌△FDC或△ABE≌△ACF.
(选证一)△BDE≌△FEC.
证明:∵△ABC是等边三角形,∴BC=AC,∠ACB=60°.
∵CD=CE,∴△EDC是等边三角形,∴DE=EC,∠CDE=∠DEC=60°,∴∠BDE=∠FEC=120°.
又∵EF=AE,∴BD=FE,∴△BDE≌△FEC.
(选证二)△BCE≌△FDC.
证明:∵△ABC是等边三角形,∴BC=AC,∠ACB=60°.
又∵CD=CE,∴△EDC是等边三角形,∴∠BCE=∠FDC=60°,DE=CE.
∵EF=AE,∴EF+DE=AE+CE,∴FD=AC=BC,∴△BCE≌△FDC.
(选证三)△ABE≌△ACF.
证明:∵△ABC是等边三角形,∴AB=AC,∠ACB=∠BAC=60°.
∵CD=CE,∴△EDC是等边三角形,∴∠AEF=∠CED=60°.
∵EF=AE,△AEF是等边三角形,∴AE=AF,∠EAF=60°,∴△ABE≌△ACF.
(2)由(1)知,△ABC、△EDC、△AEF都是等边三角形,∴∠CDE=∠ABC=∠EFA=60°,∴AB∥DF,BD∥AF,∴四边形ABDF是平行四边形.
(3)由(2)知,四边形ABDF是平行四边形,∴EF∥AB,EF≠AB,∴四边形ABEF是梯形.
过E作EG⊥AB于G,则EG=![]() ,∴
,∴![]()
![]() .
.


科目:初中数学 来源: 题型:
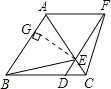
【题目】如图,△ABC的周长为64,E、F、G分别为AB、AC、BC的中点,A′、B′、C′分别为EF、EG、GF的中点,△A′B′C′的周长为_________.如果△ABC、△EFG、△A′B′C′分别为第1个、第2个、第3个三角形,按照上述方法继续作三角形,那么第n个三角形的周长是__________________.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有一根40cm的金属棒,欲将其截成x根7cm的小段和y根9cm的小段,剩余部分作废料处理,若使废料最少,则正整数x,y应分别为 ( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形ABCD中,E、F分别是边AD、CD上的点,DE=CF,AF与BE相交于O,DG⊥AF,垂足为G. 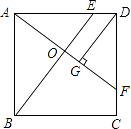
(1)求证:AF⊥BE;
(2)试探究线段AO、BO、GO的长度之间的数量关系;
(3)若GO:CF=4:5,试确定E点的位置.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有七张正面分别标有数字﹣3,﹣2,﹣1,0,1,2,3的卡片,它们除数字不同外其余全部相同.现将它们背面朝上,洗匀后从中随机抽取一张,记卡片上的数字为a,则使关于x的一元二次方程x2﹣2(a﹣1)x+a(a﹣3)=0有两个不相等的实数根,且以x为自变量的二次函数y=x2﹣(a2+1)x﹣a+2的图象不经过点(1,O)的概率是 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠ACB=90°,D是BC延长线上一点,E是BD垂直平分线与AB的交点,DE交AC于点F.求证:点E在AF的垂直平分线上.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】深化理解:
新定义:对非负实数x “四舍五入”到个位的值记为![]() ,
,
即:当n为非负整数时,如果![]() ;
;
反之,当n为非负整数时,如果![]()
例如:<0> = <0.48> = 0,<0.64> = <1.49> = 1,<2> = 2,<3.5> = <4.12> = 4,……
试解决下列问题:
(1)填空:①![]() =________(
=________(![]() 为圆周率); ②如果
为圆周率); ②如果![]() 的取值范围为____________________.
的取值范围为____________________.
(2)若关于x的不等式组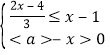 的整数解恰有3个,求a的取值范围.
的整数解恰有3个,求a的取值范围.
(3)求满足![]() 的所有非负实数x的值.
的所有非负实数x的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com