
【题目】如图,用正方形是墩垒石梯,下图分别表示垒到一、二阶梯时的情况,那么照这样垒下去
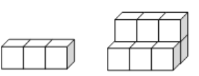
一级 二级
①填出下表中未填的两空,观察规律。
阶梯级数 | 一级 | 二级 | 三级 | 四级 |
石墩块数 | 3 | 9 |
②到第n级阶梯时,共用正方体石墩_______________块(用n的代数式表示)
【答案】①18,30;② ![]()
【解析】
分别数出一、二级台阶中正方体石墩的块数,按照这个规律求得第三、四级台阶中正方体石墩的块数,即可发现第n级台阶中正方体石墩的块数为:![]() .
.
解:①第一级台阶中正方体石墩的块数为:![]() =3;
=3;
第二级台阶中正方体石墩的块数为:3+2×3=3×(1+2)=![]() =9;
=9;
第三级台阶中正方体石墩的块数为:3+2×3+3×3=3×(1+2+3)=![]() =18;
=18;
第四级台阶中正方体石墩的块数为:3+2×3+3×3+3×4=3×(1+2+3+4)= ![]() =30;
=30;
…
依此类推,可以发现:第n级台阶中正方体石墩的块数为:3+2×3+3×3+…+3n=3×(1+2+3+…+n)=![]() .
.
阶梯级数 | 一级 | 二级 | 三级 | 四级 |
石墩块数 | 3 | 9 | 18 | 30 |
故答案为:18,30.
②按照①中总结的规律可得:当垒到第n级阶梯时,共用正方体石墩![]() 块;
块;
故答案为:![]() .
.


 尖子生新课堂课时作业系列答案
尖子生新课堂课时作业系列答案 英才计划同步课时高效训练系列答案
英才计划同步课时高效训练系列答案科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,已知矩形ABCD的三个顶点![]() 、
、![]() 、
、![]() 抛物线
抛物线![]() 过A、C两点.
过A、C两点.
![]() 直接写出点A的坐标,并求出抛物线的解析式;
直接写出点A的坐标,并求出抛物线的解析式;
![]() 动点P从点A出发
动点P从点A出发![]() 沿线段AB向终点B运动,同时点Q从点C出发,沿线段CD向终点D运动
沿线段AB向终点B运动,同时点Q从点C出发,沿线段CD向终点D运动![]() 速度均为每秒1个单位长度,运动时间为t秒
速度均为每秒1个单位长度,运动时间为t秒![]() 过点P作
过点P作![]() 交AC于点E.
交AC于点E.
![]() 过点E作
过点E作![]() 于点F,交抛物线于点
于点F,交抛物线于点![]() 当t为何值时,线段EG最长?
当t为何值时,线段EG最长?
![]() 连接
连接![]() 在点P、Q运动的过程中,判断有几个时刻使得
在点P、Q运动的过程中,判断有几个时刻使得![]() 是等腰三角形?请直接写出相应的t值.
是等腰三角形?请直接写出相应的t值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校九年级两个班,各选派10名学生参加学校举行的“汉字听写”大赛预赛,各参赛选手的成绩如下:
九(1)班:88,91,92,93,93,93,94,98,98,100;
九(2)班:89,93,93,93,95,96,96,98,98,99.
通过整理,得到数据分析表如下:
班级 | 最高分 | 平均分 | 中位数 | 众数 | 方差 |
九(1)班 | 100 | m | 93 | 93 | 12 |
九(2)班 | 99 | 95 | n | p | 8.4 |
(1)直接写出表中m、n、p的值为:m=______,n=______,p=______;
(2)依据数据分析表,有人说:“最高分在(1)班,(1)班的成绩比(2)班好.”但也有人说(2)班的成绩要好.请给出两条支持九(2)班成绩更好的理由;
(3)学校确定了一个标准成绩,等于或大于这个成绩的学生被评定为“优秀”等级,如果九(2)班有一半的学生能够达到“优秀”等级,你认为标准成绩应定为______分,请简要说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在![]() 中,∠OAB=90°,OA=AB=6,将
中,∠OAB=90°,OA=AB=6,将![]() 绕点O沿逆时针方向旋转90°得到
绕点O沿逆时针方向旋转90°得到![]() .
.
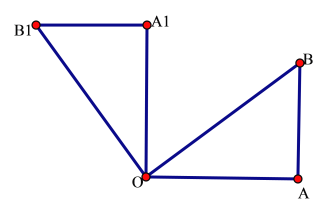
(1)线段![]() 的长是
的长是
(2)![]() 的度数是 ;
的度数是 ;
(3)求四边形的面积![]() 的面积。
的面积。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两同学玩“托球赛跑”游戏,商定:用球拍托着乒乓球从起跑线l起跑,绕过点P跑回到起跑线l(如图所示),途中乒乓球掉下时须捡起并回到掉球处继续赛跑,用时少者胜.结果:甲同学由于心急,掉了球,浪费了6秒钟,乙同学则顺利跑完.事后,乙同学说:“我俩所用的全部时间的和为50秒,捡球过程不算在内时,甲的速度是我的1.2倍.”根据图文信息,请问哪位同学获胜?
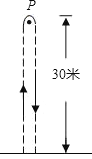
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】跃壮五金商店准备从宁云机械厂购进甲、乙两种零件进行销售.若每个甲种零件的进价比每个乙种零件的进价少2元,且用80元购进甲种零件的数量与用100元购进乙种零件的数量相同.
(1)求每个甲种零件、每个乙种零件的进价分别为多少元?
(2)若该五金商店本次购进甲种零件的数量比购进乙种零件的数量的3倍还少5个,购进两种零件的总数量不超过95个,该五金商店每个甲种零件的销售价格为12元,每个乙种零件的销售价格为15元,则将本次购进的甲、乙两种零件全部售出后,可使销售两种零件的总利润(利润=售价-进价)超过371元,通过计算求出跃壮五金商店本次从宁云机械厂购进甲、乙两种零件有几种方案?请你设计出来.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,平面直角坐标系中,点A、B、C在x轴上,点D、E在y轴上,OA=OD=2,OC=OE=4,B为线段OA的中点,直线AD与经过B、E、C三点的抛物线交于F、G两点,与其对称轴交于M,点P为线段FG上一个动点(与F、G不重合),PQ∥y轴与抛物线交于点Q.
(1)求经过B、E、C三点的抛物线的解析式;
(2)判断△BDC的形状,并给出证明;当P在什么位置时,以P、O、C为顶点的三角形是等腰三角形,并求出此时点P的坐标;
(3)若抛物线的顶点为N,连接QN,探究四边形PMNQ的形状:①能否成为菱形;②能否成为等腰梯形?若能,请直接写出点P的坐标;若不能,请说明理由.
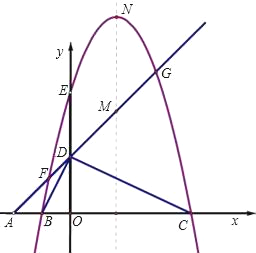
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】随着人们经济收入的不断提高,汽车已越来越多地进入到各个家庭.某大型超市为缓解停车难问题,建筑设计师提供了楼顶停车场的设计示意图.按规定,停车场坡道口上坡要张贴限高标志,以便告知车辆能否安全驶入.如图,地面所在的直线ME与楼顶所在的直线AC是平行的,CD的厚度为0.5m,求出汽车通过坡道口的限高DF的长(结果精确到0.1m,sin28°≈0.47,cos28°≈0.88,tan28°≈0.53).

查看答案和解析>>
科目:初中数学 来源: 题型:
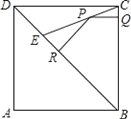
【题目】如图,E是边长为1的正方形ABCD的对角线BD上的一点,且BE=BA,P是CE上任意一点,PQ⊥BC于点Q,PR⊥BE于点R.则:(1)DE=__;(2)PQ+PR=__.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com