
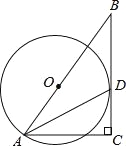
【题目】如图,⊙O的半径为4,B是⊙O外一点,连接OB,且OB=6,过点B作⊙O的切线BD,切点为D,延长BO交⊙O于点A,过点A作切线BD的垂线,垂足为C.
(1)求证:AD平分∠BAC;
(2)求CD的长.
 举一反三同步巧讲精练系列答案
举一反三同步巧讲精练系列答案 口算与应用题卡系列答案
口算与应用题卡系列答案 名师点睛字词句段篇系列答案
名师点睛字词句段篇系列答案科目:初中数学 来源: 题型:
【题目】随着互联网的发展,互联网消费逐渐深入人们生活,如图是“滴滴顺风车”与“滴滴快车”的行驶里程x(公里)与计费y(元)之间的函数关系图象,下列说法:
(1)“快车”行驶里程不超过5公里计费8元;
(2)“顺风车”行驶里程超过2公里的部分,每公里计费1.2元;
(3)A点的坐标为(6.5,10.4);
(4)从哈尔滨西站到会展中心的里程是15公里,则“顺风车”要比“快车”少用3.4元,其中正确的个数有( )

A.1个 B.2个 C.3个 D.4个
查看答案和解析>>
科目:初中数学 来源: 题型:
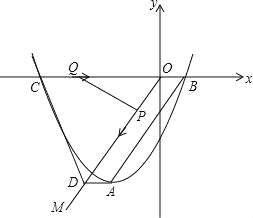
【题目】如图,顶点为A的抛物线y=a(x+2)2﹣4交x轴于点B(1,0),连接AB,过原点O作射线OM∥AB,过点A作AD∥x轴交OM于点D,点C为抛物线与x轴的另一个交点,连接CD.
(1)求抛物线的解析式、直线AB的解析式;
(2)若动点P从点O出发,以每秒1个单位长度的速度沿线段OD向点D运动,同时动点Q从点C出发,以每秒2个单位长度的速度沿线段CO向点O运动,当其中一个点停止运动时另一个点也随之停止运动.
问题一:当t为何值时,△OPQ为等腰三角形?
问题二:当t为何值时,四边形CDPQ的面积最小?并求此时PQ的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】a为有理数.定义符号“※”:当a>﹣2时,※a=﹣a;当a<﹣2时,※a=a;当a=﹣2时,※a=0.根据这种定义.则※[﹣4+※(2﹣3)]的值为( )
A. 3 B. ﹣3 C. 5 D. ﹣5
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】由于受金融危机的影响,某店经销的甲型号手机今年的售价比去年每台降价500元.如果卖出相同数量的手机,那么去年销售额为8万元,今年销售额只有6万元.
(1)今年甲型号手机每台售价为多少元?
(2)为了提高利润,该店计划购进乙型号手机销售,已知甲型号手机每台进价为1000元,乙型号手机每台进价为800元,预计用不多于1.84万元且不少于1.76万元的资金购进这两种手机共20台,请问有几种进货方案?
(3)若乙型号手机的售价为1400元,为了促销,公司决定每售出一台乙型号手机,返还顾客现金a元,而甲型号手机仍按今年的售价销售,要使(2)中所有方案获利相同,a应取何值?
查看答案和解析>>
科目:初中数学 来源: 题型:
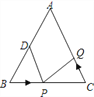
【题目】1或5 △ABC中,AB=AC=12厘米,∠B=∠C,BC=8厘米,点D为AB的中点.如果点P在线段BC上以2厘米/秒的速度由B点向C点运动,同时,点Q在线段CA上由C点向A点运动.若点Q的运动速度为v厘米/秒,则当△BPD与△CQP全等时,v的值为
A. 2 B. 3 C. 2或3 D. 1或5
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列语句正确的个数是( )
①不相交的两条直线叫做平行线;②两点之间直线最短;③只有一个公共点的两条直线叫做相交直线;④两点确定一条直线.
A. 1 B. 2 C. 3 D. 4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线AB与CD相交于点O,OP是∠BOC的平分线,OE⊥AB,OF⊥CD, 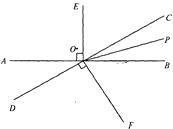
(1)图中除直角外,还有相等的角吗?请写出两对:①;② .
(2)如果∠AOD=40°,则①∠BOC=;②OP是∠BOC的平分线,所以∠COP=度;③求∠BOF的度数.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com