
【题目】如图:在正方形ABCD中,E为CD边上的一点,F为BC的延长线上一点,CE=CF。
⑴△BCE与△DCF全等吗?说明理由;
⑵若∠BEC=60o,求∠EFD。

科目:初中数学 来源: 题型:
【题目】如图,矩形ABCD中,AB=8,AD=6,将矩形ABCD折叠,使得点B落在边AD上,记为点G,BC的对应边GI与边CD交于点H,折痕为EF,则AE=时,△EGH为等腰三角形. 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,已知![]() ,
,
![]()
⑴若![]() 是
是![]() 的中点,则
的中点,则![]() _____
_____![]() ;
;
⑵若![]() 是
是![]() 的中点,则
的中点,则![]() _____
_____![]() ;
;
⑶若![]() 是
是![]() 的中点,则
的中点,则![]() ____
____![]() ;
;
⑷以此类推,若C100是AC99的中点,则AC100=____![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线L1过A(0,2),B(2,0)两点,直线L2:y=mx+b过点C(1,0),且把△AOB分成两部分,其中靠近原点的那部分是一个三角形,设此三角形的面积为S,求S关于m的函数解析式,及自变量m的取值范围.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】从甲、乙两名同学中选拔一人参加“中华好诗词”大赛,在相同的测试条件下,对两人进行了五次模拟,并对成绩(单位:分)进行了整理,计算出 ![]() =83分,
=83分, ![]() =82分,绘制成如下尚不完整的统计图表. 甲、乙两人模拟成绩统计表
=82分,绘制成如下尚不完整的统计图表. 甲、乙两人模拟成绩统计表
① | ② | ③ | ④ | ⑤ | |
甲成绩/分 | 79 | 86 | 82 | a | 83 |
乙成绩/分 | 88 | 79 | 90 | 81 | 72 |
根据以上信息,回答下列问题:
(1)a=
(2)请完成图中表示甲成绩变化情况的折线. 
(3)经计算S甲2=6,S乙2=42,综合分析,你认为选拔谁参加比赛更合适,说明理由.
(4)如果分别从甲、乙两人5次的成绩中各随机抽取一次成绩进行分析,求抽到的两个人的成绩都大于82分的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】抛物线C1:y=a(x+1)(x﹣3a)(a>0)与x轴交于A,B两点(A在B的左侧),与y轴交于点C(0,﹣3)
(1)求抛物线C1的解析式及A,B点坐标;
(2)求抛物线C1的顶点坐标;
(3)将抛物线C1向上平移3个单位长度,再向左平移n(n>0)个单位长度,得到抛物线C2 , 若抛物线C2的顶点在△ABC内,求n的取值范围. (在所给坐标系中画出草图C1)
查看答案和解析>>
科目:初中数学 来源: 题型:
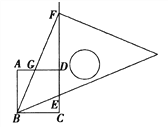
【题目】如图,正方形ABCD的边长为3,将等腰直角三角板的45°角的顶点放在点B处,直角顶点F在CD的延长线上,BF与AD交于点G,斜边与CD交于点E![]() ,若CE=1,则DG的长为( )
,若CE=1,则DG的长为( )
A. ![]() B.
B. ![]() C.
C. ![]() D. 3
D. 3
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】△ABC中,∠BAC=90°,AB=AC,点D为直线BC上一动点(点D不与B,C重合),以AD为边在AD右侧作正方形ADEF,连接CF.
(1)观察猜想
如图1,当点D在线段BC上时,
①BC与CF的位置关系为: .
②BC,CD,CF之间的数量关系为: ;(将结论直接写在横线上)
(2)数学思考
如图2,当点D在线段CB的延长线上时,结论①,②是否仍然成立?若成立,请给予证明;若不成立,请你写出正确结论再给予证明.
(3)拓展延伸
如图3,当点D在线段BC的延长线上时,延长BA交CF于点G,连接GE.若已知AB=2![]() ,CD=
,CD=![]() BC,请求出GE的长.
BC,请求出GE的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,将两块三角尺AOB与COD的直角顶点O重合在一起,若∠AOD=4∠BOC,OE为∠BOC的平分线,则∠DOE的度数为( )

A. 36° B. 45° C. 60° D. 72°
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com