
【题目】如图1,已知菱形![]() 的边长为12,
的边长为12,![]() , 点
, 点![]() 、
、![]() 分别是边
分别是边![]() 、
、![]() 上的动点(不与端点重合),且
上的动点(不与端点重合),且![]() .
.
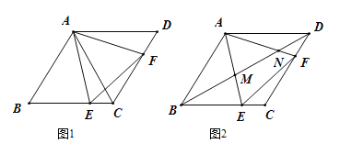
(1)求证: ![]() 是等边三角形;
是等边三角形;
(2)点![]() 、
、![]() 在运动过程中,四边形
在运动过程中,四边形![]() 的面积是否变化,如果变化,请说明理由;如果不变,请求出面积;
的面积是否变化,如果变化,请说明理由;如果不变,请求出面积;
(3)如图2,连接![]() 分别与边
分别与边![]() 、
、![]() 交于
交于![]() 、
、![]() ,当
,当![]() 时,求证:
时,求证:![]()
![]() .
.
【答案】(1)见解析;(2)不变,![]() ;(3)见解析.
;(3)见解析.
【解析】
(1)证明△ACE≌△ADF,证出AE=AF,结合![]() ,便证出△AEF是等边三角形;
,便证出△AEF是等边三角形;
(2)根据△ACE≌△ADF,则四边形![]() 的面积等于△ABC或者△ACD的面积.
的面积等于△ABC或者△ACD的面积.
(3)将△ADN绕点A顺时针旋转120°得到△ABP,连接PM.结合旋转的性质证明△MAN≌△MAP,根据四边形ABCD是菱形,∠ABC=60°,推出∠BPM=90°,即可证明结论.
(1)在菱形ABCD中,∵∠B=60°,
∴△ABC是等边三角形,∠D=∠B=60°,
∴AB=BC=AC,∠ACB=60°,
∴AC=AD,
∵![]() ,
,
∴∠CAE=∠DAF,
又∵∠D=∠ACE=60°,
∴△ACE≌△ADF,
∴AE=AF,
∴△AEF是等边三角形;
(2)点![]() 、
、![]() 在运动过程中,四边形
在运动过程中,四边形![]() 的面积不变.
的面积不变.
理由:
∵△ACE≌△ADF,
∴![]() ,即
,即![]()
![]() ;
;
(3)将△ADN绕点A顺时针旋转120°得到△ABP,连接PM.
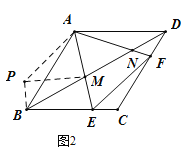
∵∠DAF=15°,∠EAF=60°,∠BAD=120°,
∴∠BAE=45°,∠BAP=∠DAF=15°,
∴∠MAN=∠MAP=60°,
∵AM=AM,AN=AP,
∴△MAN≌△MAP(SAS),
∴MN=PM,
∵四边形ABCD是菱形,∠ABC=60°,
∴∠ADN=![]() ∠ADC=30°,
∠ADC=30°,
∴∠AND=180°-15°-30°=135°,∠ANM=45°,
∴∠APB=∠AND=135°,∠APM=∠ANM=45°,
∴∠BPM=90°,
∴BP2+PM2=BM2,
∵BP=DN,PM=MN,
∴DN2+MN2=BM2.


 桃李文化快乐暑假武汉出版社系列答案
桃李文化快乐暑假武汉出版社系列答案 优秀生快乐假期每一天全新寒假作业本系列答案
优秀生快乐假期每一天全新寒假作业本系列答案 暑假接力赛新疆青少年出版社系列答案
暑假接力赛新疆青少年出版社系列答案科目:初中数学 来源: 题型:
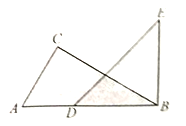
【题目】如图,把△ABC 向上平移 3 个单位长度,再向右平移 2 个单位长度,得到△A′B′C′.

(1)画出△A′B′C′;
(2)若点 P(m,n)是△ABC 某边上的点,经上述平移后,点 P 的对应点为 P′,写出点 P′ 的坐标;
(3)连接 A′A、C′C,求四边形A′ACC′的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
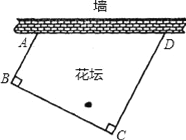
【题目】小区要用篱笆围成一个四边形花坛、花坛的一边利用足够长的墙,另三边所用的篱笆之和恰好为18米.围成的花坛是如图所示的四边形ABCD,其中∠ABC=∠BCD=90°,且BC=2AB.设AB边的长为x米.四边形ABCD面积为S平方米.
(1)请直接写出S与x之间的函数关系式(不要求写出自变量x的取值范围).
(2)当x是多少时,四边形ABCD面积S最大?最大面积是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一副三角板的三个内角分别是![]() ,
,![]() ,
,![]() 和
和![]() ,
,![]() ,
,![]() ,按如图所示叠放在一起(点
,按如图所示叠放在一起(点![]() 在同一直线上),若固定
在同一直线上),若固定![]() ,将
,将![]() 绕着公共顶点
绕着公共顶点![]() 顺时针旋转
顺时针旋转![]() 度(
度(![]() ),当边
),当边![]() 与
与![]() 的某一边平行时,相应的旋转角
的某一边平行时,相应的旋转角![]() 的值为_______.
的值为_______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下列材料:
对于多项式![]() ,如果我们把
,如果我们把![]() 代入此多项式,发现
代入此多项式,发现![]() 的值为0,这时可以确定多项式中有因式
的值为0,这时可以确定多项式中有因式![]() :同理,可以确定多项式中有另一个因式
:同理,可以确定多项式中有另一个因式![]() ,于是我们可以得到:
,于是我们可以得到:![]() .
.
又如:对于多项式![]() ,发现当
,发现当![]() 时,
时,![]() 的值为0,则多项式
的值为0,则多项式![]() 有一个因式
有一个因式![]() ,我们可以设
,我们可以设![]() ,解得
,解得![]() ,
,![]() ,于是我们可以得到:
,于是我们可以得到:![]() .
.
请你根据以上材料,解答以下问题:
(1)当![]() 时,多项式
时,多项式![]() 的值为0,所以多项式
的值为0,所以多项式![]() 有因式 ,从而因式分解
有因式 ,从而因式分解![]() .
.
(2)以上这种因式分解的方法叫试根法,常用来分解一些比较复杂的多项式.请你尝试用试根法分解多项式:①![]() ;②
;②![]() .
.
(3)小聪用试根法成功解决了以上多项式的因式分解,于是他猜想:
代数式![]() 有因式 , , ,
有因式 , , ,
所以分解因式![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在![]() 中,
中, ![]() 为
为![]() 边上一点,过点
边上一点,过点![]() 作
作![]() 交
交![]() 于点
于点![]() ,以
,以![]() 为折线,将
为折线,将![]() 翻折,设所得的
翻折,设所得的![]() 与梯形
与梯形![]() 重叠部分的面积为
重叠部分的面积为![]() .
.
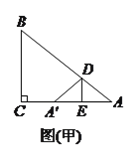
(![]() )如图(甲),若
)如图(甲),若![]() ,
, ![]() ,
, ![]() ,
, ![]() ,则
,则![]() 的值为__________.
的值为__________.
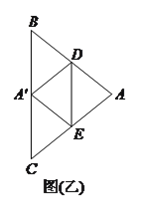
(![]() )如图(乙),若
)如图(乙),若![]() ,
, ![]() ,
, ![]() 为
为![]() 中点,则
中点,则![]() 的值为__________.
的值为__________.
(![]() )若
)若![]() ,
, ![]() ,
, ![]() ,设
,设![]() .
.
①求![]() 与
与![]() 的函数解析式.
的函数解析式.
②![]() 是否有最大值,若有,求出
是否有最大值,若有,求出![]() 的最大值;若没有,请说明理由.
的最大值;若没有,请说明理由.
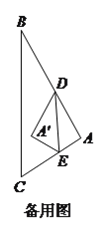
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,长方形OABC中,O为平面直角坐标系的原点,A点的坐标为(4,0),C点的坐标为(0,6),点B在第一象限内,点P从原点O出发,以每秒2个单位长度的速度沿着O﹣A﹣B﹣C﹣O的路线移动(即沿长方形移动一周).
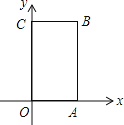
(1)写出B点的坐标;
(2)当点P移动3秒时,求三角形OAP的面积;
(3)在移动过程中,当点P到x轴距离为4个单位长度时,求点P移动的时间.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某地农民一直保持着冬种油菜的习惯,利用农闲冬种一季油菜.该地农业部门对2017年的油菜籽生产成本、市场价格、种植面积和产量等进行了调查统计,并绘制了如下的统计表与统计图(如图):
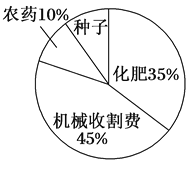
每亩生产成本 | 每亩产量 | 油菜籽市场价格 | 种植面积 |
110元 | 130千克 | 3元/千克 | 500 000亩 |
请根据以上信息解答下列问题:
(1)种植油菜每亩的种子成本是多少元?
(2)农民冬种油菜每亩获利多少元?
(3)2017年该地全县农民冬种油菜的总获利是多少元?(结果用科学记数法表示)
查看答案和解析>>
科目:初中数学 来源: 题型:
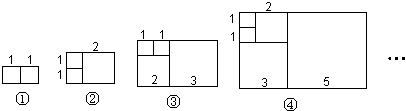
【题目】意大利著名数学家斐波那契在研究兔子繁殖问题时,发现有这样一组数:1,1,2,3,5,8,13,…,其中从第三个数起,每一个数都等于它前面两个数的和.现以这组数中的各个数作为正方形的边长值构造正方形,再分别依次从左到右取2个、3个、4个、5个…正方形拼成如上长方形,若按此规律继续作长方形,则序号为⑦的长方形周长是 .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com