
两个全等的直角三角形ABC和DEF重叠在一起,其中∠A=60°,AC=1. 固定△ABC不动,将△DEF进行如下操作:
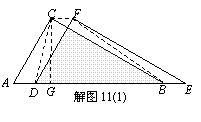
(1) 如图1,△DEF沿线段AB向右平移(即D点在线段AB内移动),连结DC、CF、FB,四边形CDBF的形状在不断的变化,但它的面积不变化,请求出其面积.
(2)如图2,当D点移到AB的中点时,请你猜想四边形CDBF的形状,并说明理由.

 (3)如图3,△DEF的D点固定在AB的中点,然后绕D点按顺时针方向旋转△DEF,使DF落在AB边上,此时F点恰好与B点重合,连结AE,请你求出sinα的值.
(3)如图3,△DEF的D点固定在AB的中点,然后绕D点按顺时针方向旋转△DEF,使DF落在AB边上,此时F点恰好与B点重合,连结AE,请你求出sinα的值.
 |
解:(1)过C点作CG⊥AB于G,
 在Rt△AGC中,∵sin60°=
在Rt△AGC中,∵sin60°=![]() ,∴
,∴![]()
∵AB=2,∴S梯形CDBF=S△ABC=![]()
(2)菱形
∵CD∥BF, FC∥BD,∴四边形CDBF是平行四边形
∵DF∥AC,∠ACD=90°,∴CB⊥DF ∴四边形CDBF是菱形
(3)解法一:过D点作DH⊥AE于H,则S△ADE=![]()
又S△ADE=![]() ,
,![]()
∴在Rt△DHE’中,sinα=![]()
解法二:∵△ADH∽△ABE 即:![]()
∴![]() ∴sinα=
∴sinα=![]()
 |
解析: 动态几何问题,是指以几何知识和图形为背景,渗入运动变化观点的一类问题,常见
的形式是:点在线段或弧线上运动、图形的翻折、平移、旋转等,解这类问题的基本策略是:
1. 动中觅静:这里的“静”就是问题中的不变量、不变关系,动中觅静就是在运动变化
中探索问题中的不变性.2.动静互化:“静”只是“动”的瞬间,是运动的一种特殊形式,动静互化就是抓住“静”的瞬间,使一般情形转化为特殊问题,从而找到“动”与“静”的关系.3.以动制动:以动制动就是建立图形中两个变量的函数关系,通过研究运动函数,用联系发展的观点来研究变动元素的关系.


 应用题作业本系列答案
应用题作业本系列答案科目:初中数学 来源: 题型:

查看答案和解析>>
科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源: 题型:
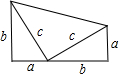 曾任美国总统的加菲尔德在《新英格兰教育日志》上发表了他提出的一个勾股定理的证明.如图,这就是他用两个全等的直角三角形拼出的图形.上面的图形整体上拼成一个直角梯形.所以它的面积有两种表示方法.既可以表示为
曾任美国总统的加菲尔德在《新英格兰教育日志》上发表了他提出的一个勾股定理的证明.如图,这就是他用两个全等的直角三角形拼出的图形.上面的图形整体上拼成一个直角梯形.所以它的面积有两种表示方法.既可以表示为查看答案和解析>>
科目:初中数学 来源: 题型:

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com