
分析 (1)根据幂的运算方法,可得21-20=2-1=1=20,22-21=4-2=2=21,23-22=8-4=4=22,据此解答即可.
(2)根据(1)中式子的规律,可得2n-2n-1=2n-1;然后根据幂的运算方法,证明第n个等式成立即可.
(3)根据2n-2n-1=2n-1,求出算式20-21-22-…-22014+22015的值是多少即可.
解答 解:(1)21-20=2-1=1=20,22-21=4-2=2=21,23-22=8-4=4=22.
(2)∵21-20=20,22-21=21,23-22=22,
∴2n-2n-1=2n-1;
证明:∵2n-2n-1=2×2n-1-2n-1=2n-1×(2-1)=2n-1,
∴2n-2n-1=2n-1成立.
(3)20-21-22-…-22014+22015
=22015-22014-22013-…-21+20
=22014-22013-…-21+20
=22013-22012-…-21+20
=…
=22-21+20
=21+20
=2+1
=3
故答案为:0、1、2.
点评 此题主要考查了探寻数列规律问题,认真观察、仔细思考,善用联想是解决这类问题的方法,注意观察总结规律,并能正确的应用规律,解答此题的关键是判断出:2n-2n-1=2n-1成立.


科目:初中数学 来源: 题型:选择题
| A. | $\left\{\begin{array}{l}a=3\\ b=-2\end{array}\right.$ | B. | $\left\{\begin{array}{l}a=-1\\ b=3\end{array}\right.$ | C. | $\left\{\begin{array}{l}a=0\\ b=2\end{array}\right.$ | D. | $\left\{\begin{array}{l}a=1\\ b=2\end{array}\right.$ |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
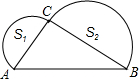 如图,已知在Rt△ABC中,∠BCA=90°,AB=10,分别以AC、BC为直径作半圆,面积分别记为S1,S2,则S1+S2=12.5π.
如图,已知在Rt△ABC中,∠BCA=90°,AB=10,分别以AC、BC为直径作半圆,面积分别记为S1,S2,则S1+S2=12.5π.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
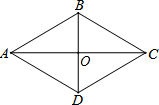 如图,在菱形ABCD中,下列结论不一定成立的是( )
如图,在菱形ABCD中,下列结论不一定成立的是( )| A. | ∠ABD=∠CBD | B. | 四边形ABCD为平行四边形 | ||
| C. | BD⊥AC | D. | △CBD是等边三角形 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com