
 如图,△ABC,∠ABC、∠ACB的三等分线交于点E、D,若∠BFC=132°,∠BGC=120°,则∠E的度数为( )
如图,△ABC,∠ABC、∠ACB的三等分线交于点E、D,若∠BFC=132°,∠BGC=120°,则∠E的度数为( )| A. | 102° | B. | 104° | C. | 106° | D. | 108° |
分析 由三角形内角和及角平分线的定义可得到关于∠DBC和∠DCB的方程组,可求得∠DBC+∠DCB,则可求得∠EBC+∠ECB,再利用三角形内角和可求得∠E的度数.
解答 解:∵∠ABC、∠ACB的三等分线交于点E、D,
∴∠FBC=2∠DBC,∠GCB=2∠DCB,
∵∠BFC=132°,∠BGC=120°,
∴∠FBC+∠DCB=180°-∠BFC=180°-132°=48°,
∠DBC+∠GCB=180°-∠BGC=180°-120°=60°,
即$\left\{\begin{array}{l}{2∠DBC+∠DCB=48°①}\\{∠DBC+2∠DCB=60°②}\end{array}\right.$,
由①+②可得:3(∠DBC+∠DCB)=108°,
∴∠EBC+∠ECB=2(∠DBC+∠DCB)=72°,
∴∠E=180°-(∠EBC+∠ECB)=180°-72°=108°,
故选D.
点评 本题主要考查三角形内角和定理,掌握三角形内角和为180°是解题的关键.


 名师点拨卷系列答案
名师点拨卷系列答案科目:初中数学 来源: 题型:解答题
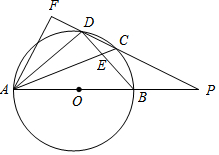 如图,四边形ABCD内接于⊙O,AB是⊙O的直径,AC和BD相交于点E,且DC2=CE•CA.
如图,四边形ABCD内接于⊙O,AB是⊙O的直径,AC和BD相交于点E,且DC2=CE•CA.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 2 | B. | 3 | C. | 4 | D. | 5 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
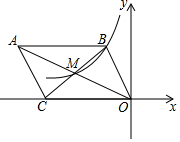 如图,在平面直角坐标系中,O为坐标原点,平行四边形ABOC的对角线交于点M,双曲线y=$\frac{k}{x}$(x<0)经过点B、M.若平行四边形ABOC的面积为12,则k=-4.
如图,在平面直角坐标系中,O为坐标原点,平行四边形ABOC的对角线交于点M,双曲线y=$\frac{k}{x}$(x<0)经过点B、M.若平行四边形ABOC的面积为12,则k=-4.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\left\{\begin{array}{l}{y+10=x-y}\\{x-y=25-x}\end{array}\right.$ | B. | $\left\{\begin{array}{l}{y-10=x-y}\\{x-y=25-y}\end{array}\right.$ | ||
| C. | $\left\{\begin{array}{l}{y-10=x-y}\\{x-y=25+x}\end{array}\right.$ | D. | $\left\{\begin{array}{l}{y-10=x-y}\\{x-y=25-x}\end{array}\right.$ |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,Rt△ABC中,∠B=90°,AB=6,BC=8,将Rt△ABC绕点C按顺时针方向旋转90°,得到Rt△A′B′C,则边AB扫过的面积(图中阴影部分)是9π.
如图,Rt△ABC中,∠B=90°,AB=6,BC=8,将Rt△ABC绕点C按顺时针方向旋转90°,得到Rt△A′B′C,则边AB扫过的面积(图中阴影部分)是9π.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com