
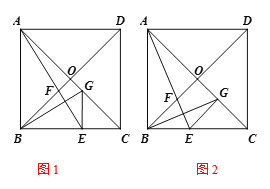
【题目】如图1,在正方形ABCD中,点O是对角线AC,BD的交点,点E在BC边上(点E不和BC的端点重合),且BE=![]() BC,连接AE交OB于点F,过点B作AE的垂线BG交OC于点G,连接GE.
BC,连接AE交OB于点F,过点B作AE的垂线BG交OC于点G,连接GE.
(1)求证:OF=OG;
(2)用含![]() 的代数式表示tan∠OBG的值;
的代数式表示tan∠OBG的值;
(3)如图2,当∠GEC=90°时,求![]() 的值.
的值.
【答案】(1) 证明见解析;(2)![]() ;(3)
;(3)![]() .
.
【解析】
(1)由正方形的性质可得AO=BO,AC⊥BD,由余角的性质可得∠FAO=∠FBG,由“ASA”可证△AOF≌△BOG,可得OF=OG;
(2)根据第一问条件推导出FG∥BC∥AD,从而由平行线分线段成比例得到![]() ,通过已知条件可推断AG=
,通过已知条件可推断AG=![]() GC,设GC=
GC,设GC=![]() ,并表示其他线段即可解决问题;
,并表示其他线段即可解决问题;
(3)根据第二问结论,使OG用OC来表示,进而使GC用BC来表示,另根据BE=![]() BC可得EC=
BC可得EC=![]() BC,从而用BC表示CG,列出方程即可解决问题.
BC,从而用BC表示CG,列出方程即可解决问题.
解:(1)证明:∵四边形ABCD是正方形,
∴OA=OB,AO⊥BO,
由∵AE⊥BG,∴∠OAF=∠OBG,
∴Rt△AOF≌Rt△BOG,
∴OF=OG;

(2)

连接FG,
∵OF=OG,AC⊥BD,
∴∠OGF=45°=∠OCB,∴FG∥BC∥AD,
∴![]() ,
,
∵BE=![]() BC=
BC=![]() AD,
AD,
∴AG=![]() GC,
GC,
设GC=![]() ,则AG=
,则AG=![]() ,AC=
,AC=![]() ,
,
∴OB=OC=![]() AC=
AC=![]() ,
,
OG=OC-GC=![]() ,
,
∴tan∠OBG=![]() =
=![]() ;
;
(3)解:如图,

当∠GEC=90°时,∵∠GCE=45°,
∴△GEC是等腰直角三角形,
∴GC=![]() EC,
EC,
∵tan∠OBG=![]() =
=![]() ,
,
∴OG=![]() OB=
OB=![]() OC,
OC,
∴GC=OC-OG=![]() OC
OC
=![]() BC,
BC,
又∵BE=![]() BC,
BC,
∴EC=BC-BE=![]() BC,
BC,
∴![]() BC=
BC=![]() BC,
BC,
即:![]() ,
,
解得:![]() 或
或![]() (舍去),
(舍去),
故![]() .
.


 单元加期末复习先锋大考卷系列答案
单元加期末复习先锋大考卷系列答案 出彩同步大试卷系列答案
出彩同步大试卷系列答案科目:初中数学 来源: 题型:
【题目】“元旦大酬宾!”,某商场设计的促销活动如下:在一个不透明的箱子里放有3张相同的卡片,卡片上分别标有“10元”、“20元”和“30元”的字样,规定:在本商场同一日内,顾客每消费满300元,就可以在箱子里摸出一张卡片,记下钱数后放回,再从中摸出一张卡片.商场根据两张卡片所标金额的和返还相等价格的购物券,购物券可以在本商场消费.某顾客刚好消费300元.
(1)该顾客最多可得到 元购物券;
(2)请你用画树状图或列表的方法,求出该顾客所获得购物券的金额不低于40元的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
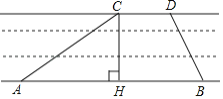
【题目】京杭大运河是世界文化遗产.综合实践活动小组为了测出某段运河的河宽(岸沿是平行的),如图,在岸边分别选定了点A、B和点C、D,先用卷尺量得AB=160m,CD=40m,再用测角仪测得∠CAB=30°,∠DBA=60°,求该段运河的河宽(即CH的长).
查看答案和解析>>
科目:初中数学 来源: 题型:
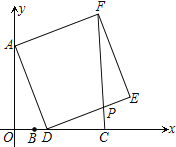
【题目】如图,在平面直角坐标系中,已知A(0,6),B(2,0),C(6,0),D为线段BC上的动点,以AD为边向右侧作正方形ADEF,连接CF交DE于点P,则CP的最大值_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】四张扑克牌的点数分别是2,5,6,8,除点数不同外,其余都相同,将它们洗匀后背面朝上放在桌上
(1)若从中随机抽取一张牌,则抽出的牌的点数是偶数的概率为 ;
(2)若随机抽取一张牌不放回,接着再抽取一张牌,请用列表法或画树状图法(只选其中一种)表示出所有可能出现的结果,并求所抽两张牌的点数都是偶数的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
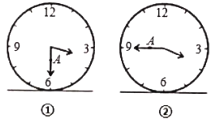
【题目】图①表示一个时钟的钟面垂直固定于水平桌面上,其中分针上有一点A,当钟面显示3点30分时,分针垂直于桌面,A点距桌面的高度为10cm.图②表示当钟面显示3点45分时,A点距桌面的高度为16cm,若钟面显示3点55分时,A点距桌面的高度为____![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠BAC=90°,AB=AC.在平面内任取一点D,连结AD(AD<AB),将线段AD绕点A逆时针旋转90°,得到线段AE,连结DE,CE,BD.
(1)直线BD和CE的位置关系是 ;
(2)猜测BD和CE的数量关系并证明;
(3)设直线BD,CE交于点P,把△ADE绕点A旋转,当∠EAC=90°,AB=2,AD=1时,直接写出PB的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2020年新冠肺炎爆发,省疾控中心组织医护人员和防疫药品赶赴湖北救援,装载防疫药品的货运飞机从机场出发,以600千米/小时的速度飞行,半小时后医护人员乘坐客运飞机从同一个机场出发,客运飞机速度是货运飞机速度的1.2倍,结果客运飞机比装载防疫药品的货运飞机迟15分钟到达湖北.
(1)设货运飞机全程飞行时间为t小时,用t表示出发的机场到湖北的路程s;
(2)求出发的机场到湖北的路程.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com