
【题目】如图,△ABC中,∠ACB=90°,AB=5cm,BC=3cm,若点P从点A出发,以每秒2cm的速度沿折线A﹣C﹣B﹣A运动,设运动时间为t秒(t>0).

(1)若点P在AC上,且满足PA=PB时,求出此时t的值;
(2)若点P恰好在∠BAC的角平分线上,求t的值.
【答案】(1)t=![]() ;(2)t=
;(2)t=![]() ;
;
【解析】
(1)设存在点P,使得PA=PB,此时PA=PB=2t,PC=4-2t,根据勾股定理列方程即可得到结论;
(2)当点P在∠CAB的平分线上时,如图,过点P作PE⊥AB于点E,此时BP=7-2t,PE=PC=2t-4,BE=5-4=1,根据勾股定理列方程即可得到结论.
(1)设存在点P,使得PA=PB,此时PA=PB=2t,
在Rt△ABC中,AC=![]() =
=![]() =4,PC=4–2t,
=4,PC=4–2t,
在Rt△PCB中,PC2+CB2=PB2,即:(4–2t)2+32=(2t)2,
解得t=![]() ,
,
∴当t=![]() 时,PA=PB;
时,PA=PB;
(2)当点P在∠BAC的平分线上时,如图,过点P作PE⊥AB于点E,
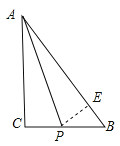
此时BP=7–2t,PE=PC=2t–4,BE=5–4=1,
在Rt△BEP中,PE2+BE2=BP2,
即:(2t–4)2+12=(7–2t)2,解得t=![]() ,
,
∴当t=![]() 时,P在∠BAC的平分线上.
时,P在∠BAC的平分线上.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】如图,△ABD和△BCD都是等边三角形纸片,AB=2,将△ABD纸片翻折,使点A落在CD的中点E处,折痕为FG,点F、G分别在边AB、AD上.
(1)求证:△FBE是直角三角形;
(2)求BF的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】点![]() 在数轴上表示的数
在数轴上表示的数![]() 满足
满足![]() ,且多项式
,且多项式![]() 是五次四项式.
是五次四项式.
(1)![]() 的值为____ ____,
的值为____ ____,![]() 的值为___ ____,
的值为___ ____,![]() 的值为____ ____;
的值为____ ____;
(2)已知点![]() 、点
、点![]() 是数轴上的两个动点,点
是数轴上的两个动点,点![]() 从点
从点![]() 出发,以
出发,以![]() 个单位/秒的速度向右运动,同时点
个单位/秒的速度向右运动,同时点![]() 从点
从点![]() 出发,以
出发,以![]() 个单位/秒的速度向左运动:
个单位/秒的速度向左运动:
① 若点![]() 和点
和点![]() 经过
经过![]() 秒后在数轴上的点
秒后在数轴上的点![]() 处相遇,求出
处相遇,求出![]() 的值和点
的值和点![]() 所表示的数;
所表示的数;
② 若点![]() 运动到点
运动到点![]() 处,动点
处,动点![]() 再出发,则
再出发,则![]() 运动几秒后这两点之间的距离为5个单位?
运动几秒后这两点之间的距离为5个单位?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,AD和AE分别是△ABC的BC边上的高和中线,点D是垂足,点E是BC的中点,规定:λA= ![]() .特别地,当点D、E重合时,规定:λA=0.另外,对λB、λC作类似的规定.
.特别地,当点D、E重合时,规定:λA=0.另外,对λB、λC作类似的规定.
(1)如图2,在△ABC中,∠C=90°,∠A=30°,求λA、λC;
(2)在每个小正方形边长均为1的4×4的方格纸上,画一个△ABC,使其顶点在格点(格点即每个小正方形的顶点)上,且λA=2,面积也为2;
(3)判断下列三个命题的真假(真命题打“√”,假命题打“×”):
①若△ABC中λA<1,则△ABC为锐角三角形;
②若△ABC中λA=1,则△ABC为直角三角形;
③若△ABC中λA>1,则△ABC为钝角三角形. .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我国是一个严重缺水的国家.为了加强公民的节水意识,某市制定了如下用水收费标准:每户每月的用水不超过6吨时,水价为每吨2元,超过6吨时,超过的部分按每吨3元收费.该市某户居民5月份用水x吨,应交水费y元.
(1)若0<x≤6,请写出y与x的函数关系式.
(2)若x>6,请写出y与x的函数关系式.
(3)如果该户居民这个月交水费27元,那么这个月该户用了多少吨水?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】李老师从“淋浴龙头”受到启发.编了一个题目: 在数轴上截取从0到3的对应线段AB,实数m对应AB上的点M,如图1;将AB折成正三角形,使点A,B重合于点P,如图2;建立平面直角坐标系,平移此三角形,使它关于y轴对称,且点P的坐标为(0,2),PM与x轴交于点N(n,0),如图3.当m= ![]() 时,求n的值.
时,求n的值.
你解答这个题目得到的n值为( )
A.4﹣2 ![]()
B.2 ![]() ﹣4
﹣4
C.![]()
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】圣诞老人上午8:00从家里出发,骑车去一家超市购物,然后从这家超市回到家中,圣诞老人离家的距离s(千米)和所经过的时间t(分钟)之间的关系如图所示,请根据图象回答问题:
(1)圣诞老人去超市途中的速度是多少?回家途中的速度是多少?
(2)圣诞老人在超市逗留了多长时间?
(3)圣诞老人在来去的途中,离家2千米处的时间是几时几分?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下面一段文字:
问题:![]() 能化为分数形式吗?
能化为分数形式吗?
探求:步骤①设![]() ,步骤②
,步骤②![]() ,
,
步骤③![]() ,则
,则![]() ,
,
步骤④![]() ,解得:
,解得:![]() .
.
根据你对这段文字的理解,回答下列问题:
(1)步骤①到步骤②的依据是什么;
(2)仿照上述探求过程,请你尝试把![]() 化为分数形式:
化为分数形式:
(3)请你将![]() 化为分数形式,并说明理由.
化为分数形式,并说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com