练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

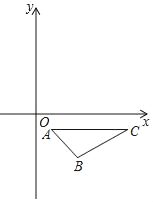
    【题目】如图，△ABC三个顶点的坐标分别是A（1，﹣1），B（2，﹣2），C（4，﹣1），将△ABC绕着原点O旋转75°，得到△A1B1C1，则点B1的坐标为（　　）

    A. （，）或（﹣，﹣） B. （，）或（﹣，﹣）

    C. （﹣，﹣）或（，） D. （﹣，﹣）或（，）

    【答案】C

    【解析】

    由A（1，﹣1），B（2，﹣2），可得O、A、B在同一条直线上，且为一、三象限的平分线，△ABC绕着原点O旋转75°，可分顺时针和逆时针两种情况讨论，结合三角函数可得B1

    解：如图

    由A（1，﹣1），B（2，﹣2），可得直线OA的解析式为：y=-x，

    OB的解析式为：y=-x，可得O、A、B三点位于同一直线上，即y=-x，

    且OAB为第二、四象限的平分线，与x轴、y轴的夹角为，

    OB==

    当△ABC绕着原点O旋转75°，当为逆时针旋转时，与x轴的夹角为，

    ==，

    ，此时点坐标为，

    同理可得当为顺时针旋转时，与y轴的夹角为,

    可得点坐标为，

    故选C.

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】如图是某教室里日光灯的四个控制开关（分别记为A、B、C、D），每个开关分别控制一排日光灯（开关序号与日光灯的排数序号不一定一致）．某天上课时，王老师在完全不知道哪个开关对应控制哪排日光灯的情况下先后随机按下两个开关．

    （1）求王老师按下第一个开关恰好能打开第一排日光灯的概率；

    （2）王老师按下两个开关恰好能打开第一排与第三排日光灯的概率是多少？请列表格或画树状图加以分析．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】某中学对学生进行“校园安全知识”知识测试，并随机抽取部分学生的成绩进行分析，将成绩分为三个等级：不合格、一般、优秀，并绘制成如下两幅统计图．

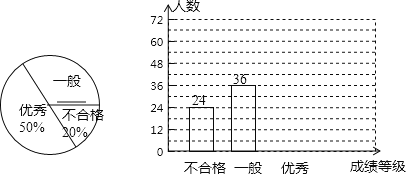
    请你根据图中所给的信息解答下列问题：

    （1）抽取的人数是____________人；补全条形统计图；

    （2）“一般”等级所在扇形的圆心角的度数是________度．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】感知：如图，平分，易知：，

    探究：（1）如图，平分．求证：．

    应用：（2）在图中，平分，如果，则____________．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图所示，n+1个直角边长为1的等腰直角三角形，斜边在同一直线上，设△B2D1C1的面积为S1，△B3D2C2的面积为S2，…，△Bn+1DnCn的面积为Sn，则S1= ，Sn= （用含n的式子表示）．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】矩形ABCD中，AB=6，AD=8，点M在对角线AC上，且AM：MC=2：3，过点M作EF⊥AC交AD于点E，交BC于点F．在AC上取一点P，使∠MEP=∠EAC，则AP的长为_____．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】每个小方格都是边长为1个单位长度的正方形，在建立平面直角坐标系后，△ABC的顶点均在格点上，

    （1）写出A、B、C的坐标．

    （2）以原点O为中心，将△ABC围绕原点O逆时针旋转180°得到△A1B1C1，画出△A1B1C1．

    （3）求（2）中C到C1经过的路径以及OB扫过的面积．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，正方形ABCD中，M为BC上一点，F是AM的中点，EF⊥AM，垂足为F，交AD的延长线于点E，交DC于点N．

    （1）求证：△ABM∽△EFA；

    （2）若AB=12，BM=5，求DE的长．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

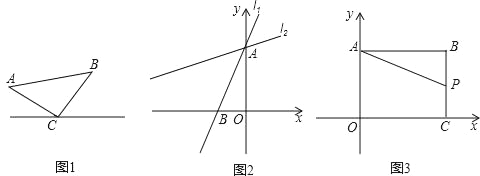
    【题目】建立模型：如图1，已知△ABC，AC=BC，∠C=90°，顶点C在直线l上．

    实践操作：过点A作AD⊥l于点D，过点B作BE⊥l于点E，求证：△CAD≌△BCE．

    模型应用：（1）如图2，在直角坐标系中，直线l1：y=x+4与y轴交于点A，与x轴交于点B，将直线l1绕着点A顺时针旋转45°得到l2．求l2的函数表达式．

    （2）如图3，在直角坐标系中，点B（8，6），作BA⊥y轴于点A，作BC⊥x轴于点C，P是线段BC上的一个动点，点Q（a，2a﹣6）位于第一象限内．问点A、P、Q能否构成以点Q为直角顶点的等腰直角三角形，若能，请求出此时a的值，若不能，请说明理由．

    查看答案和解析>>

    同步练习册答案