
【题目】问题提出:
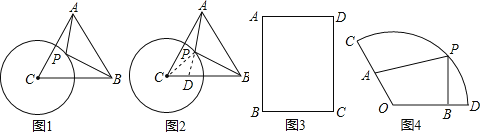
如图1,在等边△ABC中,AB=9,⊙C半径为3,P为圆上一动点,连结AP,BP,求AP+![]() BP的最小值
BP的最小值
(1)尝试解决:
为了解决这个问题,下面给出一种解题思路,通过构造一对相似三角形,将![]() BP转化为某一条线段长,具体方法如下:(请把下面的过程填写完整)
BP转化为某一条线段长,具体方法如下:(请把下面的过程填写完整)
如图2,连结CP,在CB上取点D,使CD=1,则有![]()
又∵∠PCD=∠
△ ∽△
∴![]()
∴PD=![]() BP
BP
∴AP+![]() BP=AP+PD
BP=AP+PD
∴当A,P,D三点共线时,AP+PD取到最小值
请你完成余下的思考,并直接写出答案:AP+![]() BP的最小值为 .
BP的最小值为 .
(2)自主探索:
如图3,矩形ABCD中,BC=6,AB=8,P为矩形内部一点,且PB=4,则![]() AP+PC的最小值为 .(请在图3中添加相应的辅助线)
AP+PC的最小值为 .(请在图3中添加相应的辅助线)
(3)拓展延伸:
如图4,在扇形COD中,O为圆心,∠COD=120°,OC=4.OA=2,OB=3,点P是![]() 上一点,求2PA+PB的最小值,画出示意图并写出求解过程.
上一点,求2PA+PB的最小值,画出示意图并写出求解过程.
【答案】(1)BCP,PCD,BCP,![]() ;(2)2
;(2)2![]() ;(3)作图与求解过程见解析,2PA+PB的最小值为
;(3)作图与求解过程见解析,2PA+PB的最小值为![]() .
.
【解析】
(1)连结AD,过点A作AF⊥CB于点F,AP+![]() BP=AP+PD,要使AP+
BP=AP+PD,要使AP+![]() BP最小,AP+AD最小,当点A,P,D在同一条直线时,AP+AD最小,即可求解;
BP最小,AP+AD最小,当点A,P,D在同一条直线时,AP+AD最小,即可求解;
(2)在AB上截取BF=2,连接PF,PC,AB=8,PB=4,BF=2,证明△ABP∽△PBF,当点F,点P,点C三点共线时,AP+PC的值最小,即可求解;
(3)延长OC,使CF=4,连接BF,OP,PF,过点F作FB⊥OD于点M,确定![]() ,且∠AOP=∠AOP,△AOP∽△POF,当点F,点P,点B三点共线时,2AP+PB的值最小,即可求解.
,且∠AOP=∠AOP,△AOP∽△POF,当点F,点P,点B三点共线时,2AP+PB的值最小,即可求解.
解:
(1)如图1,
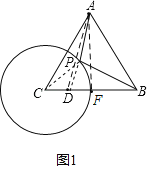
连结AD,过点A作AF⊥CB于点F,
∵AP+![]() BP=AP+PD,要使AP+
BP=AP+PD,要使AP+![]() BP最小,
BP最小,
∴AP+AD最小,当点A,P,D在同一条直线时,AP+AD最小,
即:AP+![]() BP最小值为AD,
BP最小值为AD,
∵AC=9,AF⊥BC,∠ACB=60°
∴CF=3,AF=![]() ;
;
∴DF=CF﹣CD=3﹣1=2,
∴AD=![]() ,
,
∴AP+![]() BP的最小值为
BP的最小值为![]() ;
;
故答案为:![]() ;
;
(2)如图2,

在AB上截取BF=2,连接PF,PC,
∵AB=8,PB=4,BF=2,
∴![]() ,且∠ABP=∠ABP,
,且∠ABP=∠ABP,
∴△ABP∽△PBF,
∴![]() ,
,
∴PF=![]() AP,
AP,
∴![]() AP+PC=PF+PC,
AP+PC=PF+PC,
∴当点F,点P,点C三点共线时,AP+PC的值最小,
∴CF=![]() ,
,
∴![]() AP+PC的值最小值为2
AP+PC的值最小值为2![]() ,
,
故答案为:2![]() ;
;
(3)如图3,

延长OC,使CF=4,连接BF,OP,PF,过点F作FB⊥OD于点M,
∵OC=4,FC=4,
∴FO=8,且OP=4,OA=2,
∴![]() ,且∠AOP=∠AOP
,且∠AOP=∠AOP
∴△AOP∽△POF
∴![]() ,
,
∴PF=2AP
∴2PA+PB=PF+PB,
∴当点F,点P,点B三点共线时,2AP+PB的值最小,
∵∠COD=120°,
∴∠FOM=60°,且FO=8,FM⊥OM
∴OM=4,FM=4![]() ,
,
∴MB=OM+OB=4+3=7
∴FB=![]() ,
,
∴2PA+PB的最小值为![]() .
.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】学生社团是指学生在自愿基础上结成的各种群众性文化、艺术、学术团体.不分年级、由兴趣爱好相近的同学组成,在保证学生完成学习任务和不影响学校正常教学秩序的前提下开展各种活动.某校就学生对“篮球社团、动漫社团、文学社团和摄影社团”四个社团选择意向进行了抽样调查(每人选报一类),绘制了如图所示的两幅统计图(不完整).

请根据图中信息,解答下列问题:
(1)求扇形统计图中m的值,并补全条形统计图;
(2)已知该校有1200名学生,请估计“文学社团”共有多少人?
(3)在“动漫社团”活动中,甲、乙、丙、丁、戊五名同学表现优秀,现决定从这五名同学中任选两名参加“中学生原创动漫大赛”,请用列表或画树状图的方法求出恰好选中甲、乙两位同学的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
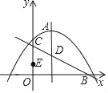
【题目】如图,二次函数y=ax2+bx+c的图象与x轴的一个交点坐标![]() ,顶点A的坐标为
,顶点A的坐标为![]() .直线
.直线![]() 交x轴于点B,交y轴于点C,与抛物线的对称轴交于点D,E为y轴上的一个动点.
交x轴于点B,交y轴于点C,与抛物线的对称轴交于点D,E为y轴上的一个动点.
(1)求这条抛物线的解析式和点D的坐标;
(2)若以C、D、E为顶点的三角形与△ACD相似,求点E的坐标;
(3)若点E关于直线BC的对称点M恰好落在抛物线上,求点M的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
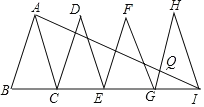
【题目】如图,已知△ABC、△DCE、△FEG、△HGI是4个全等的等腰三角形,底边BC、CE、EG、GI在同一直线上,且AB=2,BC=1,连接AI,交GH于点Q.
(1)求证:△IAB∽△ACB;
(2)求HQ:QG的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
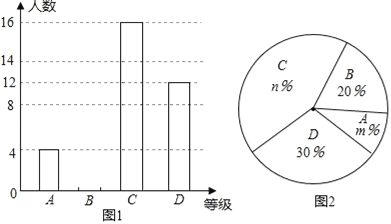
【题目】2016年3月,我市某中学举行了“爱我中国朗诵比赛”活动,根据学生的成绩划分为A、B、C、D四个等级,并绘制了不完整的两种统计图.根据图中提供的信息,回答下列问题:
(1)参加朗诵比赛的学生共有 人,并把条形统计图补充完整;
(2)扇形统计图中,m= ,n= ;C等级对应扇形有圆心角为 度;
(3)学校欲从获A等级的学生中随机选取2人,参加市举办的朗诵比赛,请利用列表法或树形图法,求获A等级的小明参加市朗诵比赛的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,直线![]() :
:![]() 与
与![]() 轴,
轴,![]() 轴分别交于
轴分别交于![]() ,
,![]() 两点,且点
两点,且点![]() ,点
,点![]() 在
在![]() 轴正半轴上运动,过点
轴正半轴上运动,过点![]() 作平行于
作平行于![]() 轴的直线
轴的直线![]() .
.
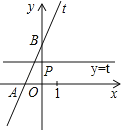
(1)求![]() 的值和点
的值和点![]() 的坐标;
的坐标;
(2)当![]() 时,直线
时,直线![]() 与直线
与直线![]() 交于点
交于点![]() ,反比例函数
,反比例函数![]() 的图象经过点
的图象经过点![]() ,求反比例函数的解析式;
,求反比例函数的解析式;
(3)当![]() 时,若直线
时,若直线![]() 与直线
与直线![]() 和(2)反比例函数的图象分别交于点
和(2)反比例函数的图象分别交于点![]() ,
,![]() ,当
,当![]() 间距离大于等于2时,求
间距离大于等于2时,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
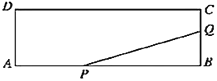
【题目】如图,在矩形![]() 中,边长
中,边长![]() ,
,![]() ,两动点
,两动点![]() 、
、![]() 分别从
分别从![]() 、
、![]() 同时出发,点
同时出发,点![]() 从
从![]() 沿
沿![]() 向
向![]() 匀速运动,每秒
匀速运动,每秒![]() ,点
,点![]() 从
从![]() 沿
沿![]() 向
向![]() 匀速运动,每秒
匀速运动,每秒![]() ,两点
,两点![]() 、
、![]() 中有一点到达矩形的顶点则运动停止.设运动时间为
中有一点到达矩形的顶点则运动停止.设运动时间为![]() 秒,
秒,![]() 的面积为
的面积为![]()
(1)求![]() 与
与![]() 的函数关系式,并写出
的函数关系式,并写出![]() 的取值范围;
的取值范围;
(2)当![]() 、
、![]() 两点运动多少秒时,
两点运动多少秒时,![]() 的面积为
的面积为![]() ;
;
(3)当![]() 取何值时,
取何值时,![]() 的面积最大?并求出其最大面积.
的面积最大?并求出其最大面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点O(0,0),A(0,1)是正方形![]() 的两个顶点,以
的两个顶点,以![]() 对角线为边作正方形
对角线为边作正方形![]() ,再以正方形的对角线
,再以正方形的对角线![]() 作正方形
作正方形![]() ,…,依此规律,则点
,…,依此规律,则点![]() 的坐标是( )
的坐标是( )

A. (-8,0) B. (0,8)
C. (0,8![]() ) D. (0,16)
) D. (0,16)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,等腰△ABC 纸板中, AB =AC=5 , BC = 2 ,P为AB上一点,过P沿直线剪下一个与△ABC 相似的小三角形纸板,恰有 3 种不同的剪法,那么BP长可以为( ).

A.3.6B.2.6C.1.6D.0.6
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com