
| A. | 没有实数根 | B. | 有实数根 | ||
| C. | 有两个相等的实数根 | D. | 有两个不相等的实数根 |
分析 先根据一次函数图象上点的坐标特征得到b=a+3,再讨论:当a=0时,b=3,方程ax2+bx+1=0化为3x+1=0,方程有解;当a≠0,计算判别式得到△=(a+1)2+8>0,根据判别式的意义判断此时方程有两个不相等的实数解,从而得到关于x的方程ax2+bx+1=0有实数解.
解答 解:∵M(a,b)是一次函数y=x+3图象上一点,
∴b=a+3,
当a=0时,b=3,方程ax2+bx+1=0化为3x+1=0,解得x=-$\frac{1}{3}$;
当a≠0,△=b2-4a=(a+3)2-4a=a2+2a+9=(a+1)2+8>0,此时方程有两个不相等的实数解;
所以关于x的方程ax2+bx+1=0有实数解.
故选B.
点评 本题考查了根的判别式:一元二次方程ax2+bx+c=0(a≠0)的根与△=b2-4ac有如下关系:当△>0时,方程有两个不相等的实数根;当△=0时,方程有两个相等的实数根;当△<0时,方程无实数根.也考查了一次函数图象上点的坐标特征.


 口算与应用题卡系列答案
口算与应用题卡系列答案 名师点睛字词句段篇系列答案
名师点睛字词句段篇系列答案科目:初中数学 来源: 题型:选择题
 在平面直角坐标系中,直线l:y=x-1与x轴交于点A1,如图所示依次作正方形A1B1C1O、正方形A2B2C2C1、…、正方形AnBnCnCn-1,使得点A1、A2、A3、…在直线l上,点C1、C2、C3、…在y轴正半轴上,则点Bn的横坐标是( )
在平面直角坐标系中,直线l:y=x-1与x轴交于点A1,如图所示依次作正方形A1B1C1O、正方形A2B2C2C1、…、正方形AnBnCnCn-1,使得点A1、A2、A3、…在直线l上,点C1、C2、C3、…在y轴正半轴上,则点Bn的横坐标是( )| A. | 2 | B. | 2n-1 | C. | 2n | D. | 2n+1 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,△ABC中,AB=AC,∠BAC=90°,在CB的延长线上取一点D,连接AD,过点A作AE⊥AD,过点C作CE⊥CB,AE与CE交于点E,连接BE,延长△ADC的中线AF交BE于点G.
如图,△ABC中,AB=AC,∠BAC=90°,在CB的延长线上取一点D,连接AD,过点A作AE⊥AD,过点C作CE⊥CB,AE与CE交于点E,连接BE,延长△ADC的中线AF交BE于点G.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
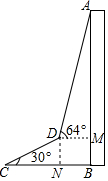 为了测量出大楼AB的高度,从距离楼底B处50米的点C(点C与楼底B在同一水平面上)出发,沿倾斜角为30°的斜坡CD前进20米到达点D,在点D处测得楼顶A的仰角为64°,求大楼AB的高度(结果精确到1米)(参考数据:sin64°≈0.9,cos64°≈0.4,tan64°≈2.1,$\sqrt{3}$≈1.7)
为了测量出大楼AB的高度,从距离楼底B处50米的点C(点C与楼底B在同一水平面上)出发,沿倾斜角为30°的斜坡CD前进20米到达点D,在点D处测得楼顶A的仰角为64°,求大楼AB的高度(结果精确到1米)(参考数据:sin64°≈0.9,cos64°≈0.4,tan64°≈2.1,$\sqrt{3}$≈1.7)查看答案和解析>>
科目:初中数学 来源: 题型:解答题
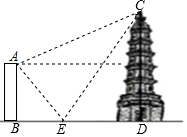 如图.大楼AB高16米,远处有一塔CD,某人在楼与塔间的平地E处测得塔顶的仰角为60°,楼顶的仰角为45°,爬到楼顶A处测得塔顶的仰角为30°,求塔CD的高度及大楼与塔之间的距离BD的长度.(结果精确到0.1米,参考数据:$\sqrt{2}≈$1.41,$\sqrt{3}≈$1.73)
如图.大楼AB高16米,远处有一塔CD,某人在楼与塔间的平地E处测得塔顶的仰角为60°,楼顶的仰角为45°,爬到楼顶A处测得塔顶的仰角为30°,求塔CD的高度及大楼与塔之间的距离BD的长度.(结果精确到0.1米,参考数据:$\sqrt{2}≈$1.41,$\sqrt{3}≈$1.73)查看答案和解析>>
科目:初中数学 来源: 题型:解答题
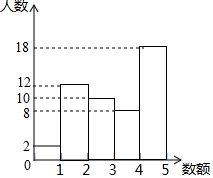 某数学兴趣小组对该校学生一天的零用钱数额(单位:元)进行了随机抽样调查,现将抽样数据分成五组(第一组:0~1元,含0元,1元;第二组:1元~2元,含2元;第三组:2元~3元,含3元;第四组:3元~4元,含4元;第五组:4元~5元,含5元),其统计图如图所示.第一组的人数、频率分别为2,0.04,第二、三、五组的频率分别为0.24,0.20,0.36.
某数学兴趣小组对该校学生一天的零用钱数额(单位:元)进行了随机抽样调查,现将抽样数据分成五组(第一组:0~1元,含0元,1元;第二组:1元~2元,含2元;第三组:2元~3元,含3元;第四组:3元~4元,含4元;第五组:4元~5元,含5元),其统计图如图所示.第一组的人数、频率分别为2,0.04,第二、三、五组的频率分别为0.24,0.20,0.36.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com