
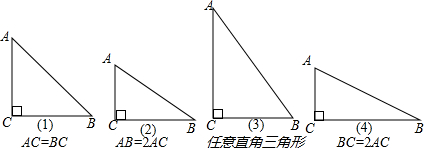
分析 (1)利用斜边上的中线,将三角形分割成两个全等的等腰直角三角形,都与原等腰直角三角形相似;
(2)过AB的中点E作AB的垂直平分线,交BC于D,则分割成的3个全等的直角三角形ACD,ADE,DEB都与原直角三角形相似,因为它们除直角外,还有一个锐角都是30°;
(3)过AB的中点分别作AC和BC的垂线,得到的4个直角三角形都与原直角三角形相似;
(4)作高CD,利用BC的中点E,分别作CD、BD的垂线即可.
解答 解:(1)如图1,取斜边AB中点D连接CD,∵AC=BC,
∴CD⊥AB,
∴等腰直角三角形ACD和CDB全等,且都与三角形ABC相似;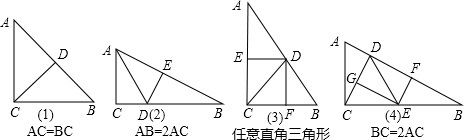
(2)如图2,作∠CAB的平分线交BC于D,作DE⊥AB于E,
∵AB=2AC,∠C=90°,
∴∠B=30°=∠CAD=∠DAB,
∴可证△ACD≌△AED≌△BED,且都与△ABC相似;
(3)如图3,取斜边AB的中点D,连接CD,则CD=AD=BD=$\frac{1}{2}$AB,
作DE⊥AC,DF⊥BC,可证△AED≌△CED≌△CFD≌△BFD,且都与△ABC相似;
(4)如图4,作CD⊥AB于D,取BC中点E,作EG⊥CD于G,EF⊥BD于F,
∴∠EGD=∠GDF=∠EFD=90°,
∴四边形DGEF是矩形,又BE=EC=AC=DE,
进而可证△ADC≌△DGE≌△EFD≌△CGE≌△EFB,且都与△ABC相似.
点评 本题一方面考查了学生的动手操作能力,另一方面考查了学生的空间想象能力,重视知识的发生过程,让学生体验学习的过程,进一步加深了对全等三角形判定的运用.


 期末冲刺100分创新金卷完全试卷系列答案
期末冲刺100分创新金卷完全试卷系列答案科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
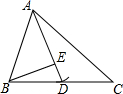 如图,在△ABC中,AC>AB,以点A为圆心、AB长为半径的弧恰交BC于点D,连接AD,过点B作BE⊥AD,垂足为E.
如图,在△ABC中,AC>AB,以点A为圆心、AB长为半径的弧恰交BC于点D,连接AD,过点B作BE⊥AD,垂足为E.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
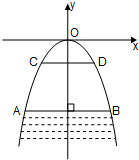 有一座抛物线形拱桥,以坐标原点O为抛物线的顶点,以y轴为抛物线的对称轴建立如图所示的坐标系,桥下面在正常水位AB时,宽20米,水位上升3米就达到警戒线CD,这时水面宽为10米.求抛物线的解析式及警戒线CD到拱桥顶O的距离.
有一座抛物线形拱桥,以坐标原点O为抛物线的顶点,以y轴为抛物线的对称轴建立如图所示的坐标系,桥下面在正常水位AB时,宽20米,水位上升3米就达到警戒线CD,这时水面宽为10米.求抛物线的解析式及警戒线CD到拱桥顶O的距离.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
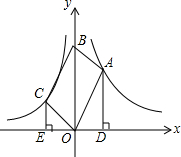 在平面直角坐标系xOy中,函数y=$\frac{{k}_{1}}{x}$(k1>0,x>0)、函数y=$\frac{{k}_{2}}{x}$(k2<0,x<0)的图象分别经过?OABC的顶点A、C,点B在y轴正半轴上,AD⊥x轴于点D,CE⊥x轴于点E,若|k1|:|k2|=9:4,则AD:CE的值为( )
在平面直角坐标系xOy中,函数y=$\frac{{k}_{1}}{x}$(k1>0,x>0)、函数y=$\frac{{k}_{2}}{x}$(k2<0,x<0)的图象分别经过?OABC的顶点A、C,点B在y轴正半轴上,AD⊥x轴于点D,CE⊥x轴于点E,若|k1|:|k2|=9:4,则AD:CE的值为( )| A. | 4:9 | B. | 2:3 | C. | 3:2 | D. | 9:4 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com