


科目:初中数学 来源: 题型:
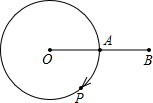 (2008•南平质检)如图,A是半径为6cm的⊙O上的定点,动点P从A出发,以πcm/s的速度沿圆周按顺时针方向运动,当点P回到A时立即停止运动.设点P运动时间为t(s)
(2008•南平质检)如图,A是半径为6cm的⊙O上的定点,动点P从A出发,以πcm/s的速度沿圆周按顺时针方向运动,当点P回到A时立即停止运动.设点P运动时间为t(s)查看答案和解析>>
科目:初中数学 来源:2009年浙江省绍兴市绍兴县兰亭镇中数学中考模拟试卷(解析版) 题型:解答题
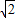 )(其中m>0),在BC边上选取适当的点E和点F,将△OCE沿OE翻折,得到△OGE;再将△ABF沿AF翻折,恰好使点B与点G重合,得到△AGF,且∠OGA=90度.
)(其中m>0),在BC边上选取适当的点E和点F,将△OCE沿OE翻折,得到△OGE;再将△ABF沿AF翻折,恰好使点B与点G重合,得到△AGF,且∠OGA=90度.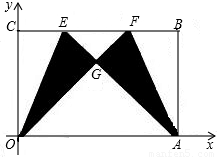
查看答案和解析>>
科目:初中数学 来源:2009年广东省茂名十中初中数学综合练习试卷(6)(解析版) 题型:解答题
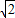 )(其中m>0),在BC边上选取适当的点E和点F,将△OCE沿OE翻折,得到△OGE;再将△ABF沿AF翻折,恰好使点B与点G重合,得到△AGF,且∠OGA=90度.
)(其中m>0),在BC边上选取适当的点E和点F,将△OCE沿OE翻折,得到△OGE;再将△ABF沿AF翻折,恰好使点B与点G重合,得到△AGF,且∠OGA=90度.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com