
��ͼ����ƽ��ֱ������ϵ�У�������y=ax2+ bx+4��x���һ������ΪA����2��0������y��Ľ���ΪC���Գ�����x=3���Գ�����x�ύ�ڵ�B��
bx+4��x���һ������ΪA����2��0������y��Ľ���ΪC���Գ�����x=3���Գ�����x�ύ�ڵ�B��
��1���������ߵĺ�������ʽ��
��2������B��C��ֱ��lƽ�ƺ��������߽��ڵ�M����x�ύ�ڵ�N������B��C��M��NΪ������ı�����ƽ���ı���ʱ�������M�����ꣻ
��3������D��x���ϣ������������Ƿ���ڵ�P��ʹ�á�PBD�ա�PBC�������ڣ�ֱ��д����P�����ꣻ�������ڣ���˵�����ɣ�
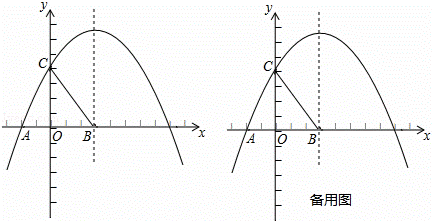
�⣺��1����������y=ax2+bx+4��x����A����2��0����
��0=4a��2b+4��
�߶Գ�����x=3��
�ੁ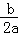 =3����6a+b=0��
=3����6a+b=0��
������a��b�ķ���������� a=��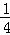 ��b=
��b=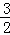 ��
��
��������Ϊy=��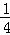 x2+
x2+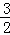 x+4��
x+4��
��2�����ı���Ϊƽ���ı��Σ���BC��MN��
��BC=MN��
 ��N����M�����·�����M����ƽ��4����λ������ƽ��2����λ��N�غϣ�
��N����M�����·�����M����ƽ��4����λ������ƽ��2����λ��N�غϣ�
��M��x����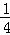 x2+
x2+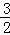 x+4������N��x+2����
x+4������N��x+2����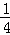 x2+
x2+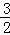 x����
x����
��N��x���ϣ�
�ੁ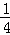 x2+
x2+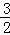 x=0��
x=0��
��� x=0��M��C�� �ϣ���ȥ������x=6��
�ϣ���ȥ������x=6��
��xM=6��
��M��6��4����
��M����N���·�����N����ƽ��4����λ������2����λ��M�غϣ�
��M��x����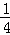 x2+
x2+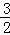 x+4������N��x��2����
x+4������N��x��2����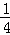 x2+
x2+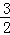 x+8����
x+8����
��N��x���ϣ�
�ੁ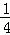 x2+
x2+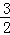 x+8=0��
x+8=0��
��� x=3��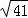 ����x=3+
����x=3+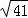 ��
��
��xM=3��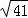 ����3+
����3+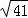 ��
��
��M��3��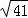 ����4����3+
����4����3+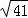 ����4��
����4��
����������M��������6��4����3��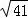 ����4����3+
����4����3+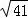 ����4����
����4����
��3����OC=4��OB=3��
��BC=5��
�����PBD�ա�PBC����ôBD=BC=5��
��D��x���ϣ�
��D����2��0����8��0����
�ٵ�DΪ ����2��0��ʱ������CD����B��ֱ��BEƽ�֡�DBC��CD��E������������P1��P2��
����2��0��ʱ������CD����B��ֱ��BEƽ�֡�DBC��CD��E������������P1��P2��
��ʱ��P1BC�ա�P1BD����P2BC�ա�P2BD��
��BC=BD��
��EΪCD���е㣬��E����1��2����
���E����1��2����B��3��0����ֱ��Ϊy=kx+b����  ��
��
���  ��
��
��BE��y=��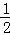 x+
x+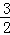 ��
��
��P��x��y��������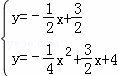 ��
��
��� 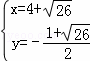 ����
����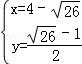 ��
��
��P1��4+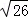 ��
��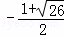 ����P2��4��
����P2��4��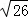 ��
��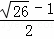 ����
����
�ڵ�DΪ��8��0��ʱ������CD����B��ֱ��BFƽ�֡�DBC��CD��F������������P3��P4��
��ʱ��P3BC�ա�P3BD����P4BC�ա�P4BD��
��BC=BD��
��FΪCD���е㣬��E�� 4��2����
4��2����
���E��4��2����B��3��0����ֱ��Ϊy=kx+b����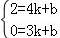 ��
��
��� 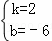 ��
��
��BF��y=2x��6��
��P��x��y��������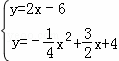 ��
��
��� 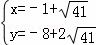 ��
�� 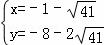 ��
��
��P3����1+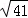 ����8+2
����8+2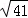 ����P4����1��
����P4����1��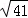 ����8��2
����8��2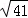 ����
����
������������P��������4+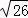 ��
��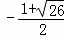 ����4��
����4��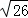 ��
��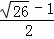 ����1+
����1+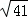 ����8+2
����8+2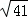 ����1��
����1��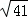 ����8��2
����8��2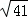 ����
����


 ��У����ϵ�д�
��У����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
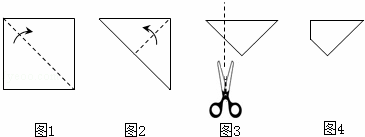
��һ��������ֽƬ����ͼ1��ͼ2��ʾ�ķ�����ۣ�Ȼ����ͼ3�е������õõ�ͼ4����ͼ4��ֽƬչ����ƽ���ٵõ���ͼ���ǣ�������
| �� | A�� |
| B�� |
| C�� |
| D�� |
|
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
��ͼ����ƽ��ֱ������ϵ�У�ֱ��l��x���ཻ�ڵ�M����y���ཻ�ڵ�N��Rt��MON������Ϊ��A������2��������������y=��x��0����ͼ�����A��
��1����ֱ��l�Ľ���ʽ��
��2���ں���y=��x��0����ͼ����ȡ���ڵ�A��һ��B����BC��x���ڵ�C������OB��ֱ��l�ڵ�P������ONP������ǡ�OBC�����3�������P�����꣮

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
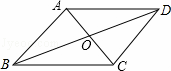
��ͼ�����ı���ABCD�У��Խ���AC��BD���ڵ�O��OA=OC��OB=OD������һ������ʹ�ı���ABCD�����Σ���ô�����ӵ�����������������д��һ�����ɣ���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
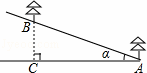
��ͼ����ɽ����ֲ������֪ɽ�µ���б�Ǧ���20�㣬С����ֲ������������������AB��6�ף�Ҫ���������������ˮƽ����AC��5.3��5.7��Χ�ڣ���С����ֲ�����������Ƿ�������Ҫ��
���ο����ݣ�sin20���0.34��cos20���0.94��tan20���0.36��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
С����ö�Ԫһ�η�����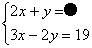 �Ľ�Ϊ
�Ľ�Ϊ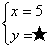 �����ڲ�С�ģ�����������īˮ���պ���ס����������͡���= ����=
�����ڲ�С�ģ�����������īˮ���պ���ס����������͡���= ����=
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com