
【题目】如图,点P是![]() 上一动点,连接AP,作∠APC=45°,交弦AB于点C.AB=6cm.
上一动点,连接AP,作∠APC=45°,交弦AB于点C.AB=6cm.
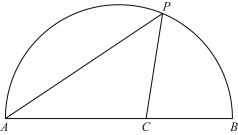
小元根据学习函数的经验,分别对线段AP,PC,AC的长度进行了测量.
下面是小元的探究过程,请补充完整:
(1)下表是点P是![]() 上的不同位置,画图、测量,得到线段AP,PC,AC长度的几组值,如下表:
上的不同位置,画图、测量,得到线段AP,PC,AC长度的几组值,如下表:
AP/cm | 0 | 1.00 | 2.00 | 3.00 | 4.00 | 5.00 | 6.00 |
PC/cm | 0 | 1.21 | 2.09 | 2.69 | m | 2.82 | 0 |
AC/cm | 0 | 0.87 | 1.57 | 2.20 | 2.83 | 3.61 | 6.00 |
①经测量m的值是 (保留一位小数).
②在AP,PC,AC的长度这三个量中,确定![]() 的长度是自变量,
的长度是自变量,![]() 的长度和 的长度都是这个自变量的函数;
的长度和 的长度都是这个自变量的函数;
(2)在同一平面直角坐标系xOy中,画出(1)中所确定的函数图象;

(3)结合函数图象,解决问题:当△ACP为等腰三角形时,AP的长度约为 cm(保留一位小数).
【答案】(1)①3.0;②AP的长度是自变量,PC的长度和AC的长度都是这个自变量的函数;(答案不唯一);(2)见解析; (3)2.3或4.2
【解析】
(1)①根据题意AC的值分析得出PC的值接近于半径;
②由题意AP的长度是自变量,分析函数值即可;
(2)利用描点法画出函数图像即可;
(3)利用数形结合的思想解决问题即可.
解:(1)①AC=2.83可知PC接近于半径3.0;
②AP的长度是自变量,PC的长度和AC的长度都是这个自变量的函数;(答案不唯一)
(2)如图(答案不唯一,和(1)问相对应);
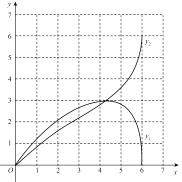

(3)结合图像根据AP=PC以及AC=PC进行代入分析可得AP为2.3或4.2


科目:初中数学 来源: 题型:
【题目】如图1,点C是线段AB上一点,AC=![]() AB,BC为⊙O的直径.
AB,BC为⊙O的直径.
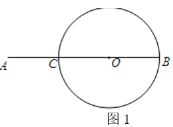
(1)在图1直径BC上方的圆弧上找一点P,使得PA=PB;(用尺规作图,保留作图痕迹,不要求写作法)
(2)连接PA,求证:PA是⊙O的切线;
(3)在(1)的条件下,连接PC、PB,∠PAB的平分线分别交PC、PB于点D、E.求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC是等腰直角三角形,∠ACB=90°,BC=AC,把△ABC绕点A按顺时针方向旋转45°后得到△AB’C’,若AB=2,则线段BC在上述旋转过程中所扫过部分(阴影部分)的面积是___________ (结果保留π)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知AB是⊙O的直径,点C、D在⊙O上,∠D=60°,且AB=6,过O点作OE⊥AC,垂足为E.
(1)求OE的长;
(2)若OE的延长线交⊙O于点F,求弦AF、AC和弧CF围成的图形(阴影部分)的面积.(结果精确到0.01)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点D、E分别为△ABC的边AB、AC上的点,BE与CD相交于点O,现有四个条件:①AB=AC;②OB=OC;③∠ABE=∠ACD;④BE=CD,选择其中2个条件作为题设,余下2个条件作为结论,所有命题中,真命题的个数为( )
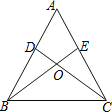
A. .3B. .4C. .5D. 、6
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=ax2+bx+c(a≠0)的对称轴为直线x=-2,与x轴的一个交点在(-3,0)和(-4,0)之间,其部分图象如图所示.则下列结论:①4a-b=0;②c<0;③-3a+c>0;④4a-2b>at2+bt(t为实数);⑤点![]() ,
,![]() ,
,![]() 是该抛物线上的点,则y1<y2<y3.其中正确结论的个数是( )
是该抛物线上的点,则y1<y2<y3.其中正确结论的个数是( )
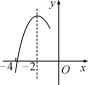
A.4B.3C.2D.1
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】草莓是种老少皆宜的食品,深受市民欢迎.今年3月份,甲,乙两超市分别用3000元以相同的进价购进质量相同的草莓.甲超市销售方案是:将草莓按大小分类包装销售,其中大草莓400千克,以进价的2倍价格销售,剩下的小草莓以高于进价的10%销售.乙超市销售方案是:不将草莓按大小分类,直接包装销售,价格按甲超市大、小两种草莓售价的平均数定价.若两超市将草莓全部售完,其中甲超市获利2100元(其他成本不计).
(1)草莓进价为每千克多少元?
(2)乙超市获利多少元?并比较哪种销售方式更合算.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com