
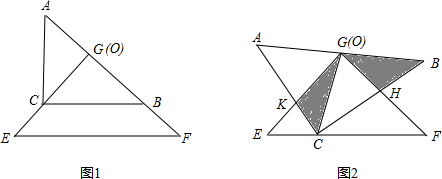
把两个全等的等腰直角三角板ABC和EFG(其直角边长均为4)叠放在一起(如图1),且使三角板EFG的直角顶点G与三角板ABC斜边的中点O重合.现将三角板EFG绕点O顺时针旋转α(旋转角α满足条件:0°<α<90°),如图2,四边形CHGK是旋转过程中两个三角板的重叠部分.

在上述旋转过程中,BH与CK有怎样的数量关系?四边形CHGK的面积有何变化?请证明你的发现.
|
解:BH=CK,四边形CHGK的面积没有变化. 证明:如图,
因为△ABC是等腰直角三角形,点O为AB的中点,所以AC=BC,CG=BG,CG⊥AB.所以△ACG≌△CBG.所以∠ACG=∠B=45°. 如图,
因为∠BGH与∠CGK均为旋转角,所以∠BGH=∠CGK. 所以△CGK≌△BGH. 所以△CGK可以看作是由△BGH绕点O顺时针旋转90°得到的. 所以BH=CK,S△CGK=S△BGH. 所以S四边形CHGK=S△CGK+S△CGH=S△BGH+S△CGH= S△CBG= 故在旋转过程中四边形CHGK的面积没有变化,始终为4. 点评:以上两个例子,利用旋转变换的性质,将不规则的重叠部分的面积转化为规则图形的面积,实现了由一般到特殊的转化,体现了转化思想,希望同学们深刻领会,灵活运用. |


 互动课堂系列答案
互动课堂系列答案 激活思维智能训练课时导学练系列答案
激活思维智能训练课时导学练系列答案科目:初中数学 来源: 题型:
 把两个全等的等腰直角三角形ABC和EFG(其直角边长均为4)叠放在一起(如图①),且使三角板EFG的直角顶点G与三角板ABC的斜边中点O重合.现将三角板EFG绕O点逆时针旋转(旋转角α满足条件:0°<α<90°),四边形CHGK是旋转过程中两三角板的重叠部分(如图②).
把两个全等的等腰直角三角形ABC和EFG(其直角边长均为4)叠放在一起(如图①),且使三角板EFG的直角顶点G与三角板ABC的斜边中点O重合.现将三角板EFG绕O点逆时针旋转(旋转角α满足条件:0°<α<90°),四边形CHGK是旋转过程中两三角板的重叠部分(如图②).| 5 | 16 |
查看答案和解析>>
科目:初中数学 来源: 题型:
查看答案和解析>>
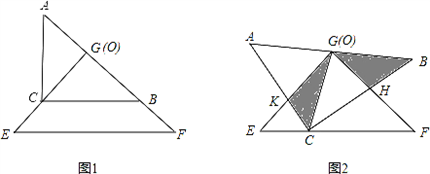
科目:初中数学 来源:云南省期末题 题型:解答题
查看答案和解析>>
科目:初中数学 来源:第25章《图形的变换》常考题集(13):25.2 旋转变换(解析版) 题型:解答题
 ?若存在,求出此时x的值;若不存在,说明理由.
?若存在,求出此时x的值;若不存在,说明理由.
查看答案和解析>>
科目:初中数学 来源:第23章《旋转》常考题集(04):23.1 图形的旋转(解析版) 题型:解答题
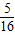 ?若存在,求出此时x的值;若不存在,说明理由.
?若存在,求出此时x的值;若不存在,说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com