
����Ŀ����ѧУ��չ�����װ�������У�С��ͬѧ����������ڼ����һ����ḣ���������A��B��C��D�����鿯��Ϊ���˽������鿯�����������С�������·��������鿯��������������ͳ�ƣ�С��ͨ���ɼ����ݣ�������������������ͳ��ͼ������ͼ���������������������Ϣ����������⣺
�鿯���� | Ƶ�� | Ƶ�� |
A | �� �� | 0.25 |
B | 1000 | 0.20 |
C | 750 | 0.15 |
D | 2000 | �� �� |
��1�����Ƶ�ʷֲ����еĿո�ȫƵ���ֲ�ֱ��ͼ��
��2���������ƻ������������鿯6000�ᣬ�������B���鿯Ӧ�ɹ����ٲ�Ϻ��ʣ�
��3����Ե��������������С��ͬѧ���������һ���������Ľ��飮
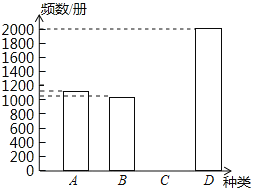
���𰸡���1������������2��B���鿯Ӧ�ɹ�1200��Ϻ��ʣ���3���ڹ���ʱӦ�ö��D���鿯��
��������
��1����ͳ�Ʊ���ֱ��ͼ��֪��D���鿯��Ƶ��Ϊ1-0.25-0.20-0.15=0.40��A���鿯��Ƶ��Ϊ1250��
��2���ƻ������������鿯6000�ᣬ��B���鿯Ӧ�ɹ�6000��0.20=1200�
��3���ڹ���ʱӦ�ö��D���鿯��ֻҪ�������ɣ���
�⣺��1����ɱ����ֱ��ͼ����ͼ��
�鿯���� | Ƶ�� | Ƶ�� |
A | 1250 | 0.25 |
B | 1000 | 0.20 |
C | 750 | 0.15 |
D | 2000 | 0.4 |
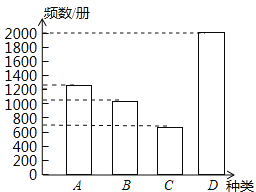
��2��6000��0.2��1200���ᣩ��
��B���鿯Ӧ�ɹ�1200��Ϻ��ʣ�
��3���ڹ���ʱӦ�ö��D���鿯��



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������ij�̳�����ͣ������5������ڣ�ÿ���糿7�㿪ʼ����ͣ���Ҵ�ʱ��λ������Ϊ90%����ÿ������ڵij������������ٳ��������£��������2�����ں�3�����ڣ�6Сʱ����ǡ��ͣ�����������3�����ں�2�����ڣ�3Сʱ����ǡ��ͣ����2019���������ڼ䣬�����̳��������࣬�糿7��ʱ�ij�λ�����ʱ�Ϊ60%����Ϊ������죬ֻ�ܿ���1�����ں�1�����ڣ�����糿7�㿪ʼ����______Сʱ����ǡ��ͣ����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪������![]() ����
����![]() ��
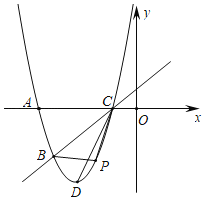
��![]() ���㣬��x�����һ������ΪC������ΪD������CD��
���㣬��x�����һ������ΪC������ΪD������CD��
��1����������ߵı���ʽ��
��2����PΪ����������һ���㣨���B��C���غϣ������P�ĺ�����Ϊt��
�ٵ���P��ֱ��BC���·��˶�ʱ����![]() ����������ֵ��
����������ֵ��
�ڸ����������Ƿ���ڵ�P��ʹ��![]() �����ڣ�������е�P�����ꣻ�������ڣ���˵�����ɣ�
�����ڣ�������е�P�����ꣻ�������ڣ���˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ƽ��ֱ������ϵ�У�����y=![]() (k��0��x��0)��ͼ����ȱ�������OAB�ı�OA��AB�ֱ��ڵ�M��N����OM=2MA����AB=3����ô��N�ĺ�����Ϊ(����)
(k��0��x��0)��ͼ����ȱ�������OAB�ı�OA��AB�ֱ��ڵ�M��N����OM=2MA����AB=3����ô��N�ĺ�����Ϊ(����)
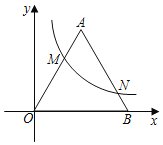
A.![]() B.
B.![]() C.4D.6
C.4D.6
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ʾ����֪������ABCD��������AEFG������DG��BE��
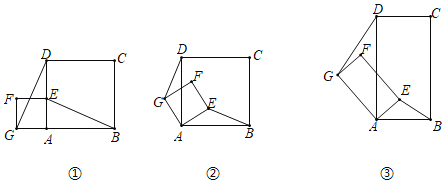
��1�����֣���������AEFG�Ƶ�A��ת����ͼ����ʾ��
���߶�DG��BE֮���������ϵ���� ����
��ֱ��DG��ֱ��BE֮���λ�ù�ϵ���� ����
��2��̽������ͼ����ʾ�����ı���ABCD���ı���AEFG��Ϊ���Σ���AD��2AB��AG��2AEʱ�����������Ƿ��������˵�����ɣ�
��3��Ӧ�ã��ڣ�2��������£�����BG��DE����AE��1��AB��2����BG2+DE2��ֵ��ֱ��д���������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
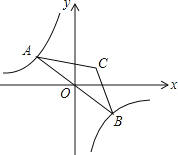
����Ŀ����ͼ����֪����������y����![]() ��ͼ����ֱ��y��kx��k��0���ཻ�ڵ�A��B����ABΪ�������������Σ�ʹ��ACB��120�����ҵ�C��λ������k�IJ�ͬȡֵ�������仯������Cʼ����ijһ����ͼ���ϣ������ͼ������Ӧ�ĺ�������ʽΪ__��
��ͼ����ֱ��y��kx��k��0���ཻ�ڵ�A��B����ABΪ�������������Σ�ʹ��ACB��120�����ҵ�C��λ������k�IJ�ͬȡֵ�������仯������Cʼ����ijһ����ͼ���ϣ������ͼ������Ӧ�ĺ�������ʽΪ__��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���������![]() ��һԪ���η���
��һԪ���η���![]() ������ʵ������������һ��Ϊ��һ����2������������ķ���Ϊ���������̡������¹��ڱ������̵�˵��������ȷ���ǣ� ��
������ʵ������������һ��Ϊ��һ����2������������ķ���Ϊ���������̡������¹��ڱ������̵�˵��������ȷ���ǣ� ��
A.����![]() �DZ������̣�
�DZ������̣�
B.��![]() �DZ������̣���
�DZ������̣���![]() ��
��
C.������![]() �DZ������̣�����������
�DZ������̣�����������![]() ����������
����������![]() �ϣ���
�ϣ���![]() ��һ����Ϊ
��һ����Ϊ![]() ��
��
D.����![]() �ڷ���������
�ڷ���������![]() ��ͼ���ϣ������
��ͼ���ϣ������![]() �ķ���
�ķ���![]() �DZ������̣�
�DZ������̣�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
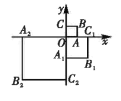
����Ŀ����ͼ����ƽ��ֱ������ϵ![]() �У�������
�У�������![]() �Ķ���
�Ķ���![]() �ֱ���
�ֱ���![]() ��
��![]() ���ϣ���
���ϣ���![]() ����������
����������![]() ��ԭ��
��ԭ��![]() ˳ʱ����ת
˳ʱ����ת![]() ����
����![]() ���õ�������
���õ�������![]() ���ٽ�����
���ٽ�����![]() ��ԭ��
��ԭ��![]() ˳ʱ����ת
˳ʱ����ת![]() ����
����![]() ���õ�������
���õ�������![]() ���Դ˹��ɣ��õ�������
���Դ˹��ɣ��õ�������![]() �����
�����![]() ������Ϊ__________��
������Ϊ__________��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ƽ��ֱ������ϵ�У�������![]() ��
��![]() �ύ��
�ύ��![]() ��
��![]() ���㣨��
���㣨��![]() �ڵ�
�ڵ�![]() ��ࣩ��������
��ࣩ��������![]() ��ֱ��
��ֱ��![]() ��
��![]() ��
��![]() �ύ�ڵ�
�ύ�ڵ�![]() ���������ߵ���һ������Ϊ
���������ߵ���һ������Ϊ![]() ����
����![]() ��
��
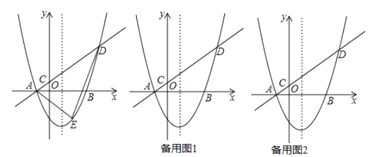
��1��ֱ��д����![]() �����꣬���ú�
�����꣬���ú�![]() ��ʽ�ӱ�ʾֱ��
��ʽ�ӱ�ʾֱ��![]() �ĺ�������ʽ������
�ĺ�������ʽ������![]() ��
��![]() �ú�
�ú�![]() ��ʽ�ӱ�ʾ����
��ʽ�ӱ�ʾ����
��2����![]() Ϊֱ��
Ϊֱ��![]() �·���������һ�㣬��
�·���������һ�㣬��![]() ����������ֵΪ
����������ֵΪ![]() ʱ���������ߵĺ�������ʽ��
ʱ���������ߵĺ�������ʽ��
��3�����![]() �������߶Գ����ϵ�һ�㣬��
�������߶Գ����ϵ�һ�㣬��![]() ���������ϣ��Ե�
���������ϣ��Ե�![]() ��
��![]() ��
��![]() ��
��![]() Ϊ������ı����ܷ�Ϊ���Σ����ܣ������
Ϊ������ı����ܷ�Ϊ���Σ����ܣ������![]() �����ꣻ�����ܣ���˵�����ɣ�
�����ꣻ�����ܣ���˵�����ɣ�
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com