先阅读下面的内容，再解决问题，
例题：若m2＋2mn＋2n2－6n＋9＝0，求m和n的值．
解：∵m2＋2mn＋2n2—6n＋9＝0
∴m2＋2mn＋n2＋n2－6n＋9＝0
∴(m＋n)2＋(n－3)2＝0
∴m＋n＝0
，n－3＝0
∴m＝－3，n＝3
问题：(1)若x2＋2y2－2xy＋4y＋4＝0，求xy的值．
(2)已知△ABC的三边长a,b,c都是正整数，且满足a2＋b2－6a－6b＋18＋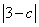
＝0，请问△ABC是怎样形状的三角形?
科目：初中数学 来源： 题型：
甲型H1N1流感病毒的直径大约为0.000 000 081米，则这个数用科学记数法表示为（ ）
A．8.1×10-6m B．81×10-9m C．8.1×10-8m D． 0.81×10-7m
查看答案和解析>>
科目：初中数学 来源： 题型：
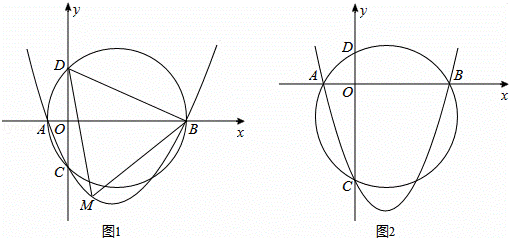
如图，已知抛物线y=ax2+bx+c（a＞0，c＜0）交x轴于点A，B，交y轴于点C，设过点A，B，C三点的圆与y轴的另一个交点为D．
（1）如图1，已知点A，B，C的坐标分别为（﹣2，0），（8，0），（0，﹣4）；
①求此抛物线的表达式与点D的坐标；
②若点M为抛物线上的一动点，且位于第四象限，求△BDM面积的最大值；
（2）如图2，若a=1，求证：无论b，c取何值，点D均为顶点，求出该定点坐标．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
﹣1=0有增根，则a的值为 
的解为
，由于不小心，滴上了两滴墨水，刚好遮住了两个数●和★，则●= ，★= 
－
＝ .