
【题目】如图1,四边形ABCD中,AD∥BC,AB⊥BC,点E在边AB上,∠DEC=900,且DE=EC.
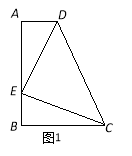
(1)求证:△ADE≌△BEC;
(2)若AD=a,AE=b,DE=c,请用图1证明勾股定理:a2+b2=c2;
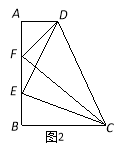
(3)线段AB上另有一点F(不与点E重合),且DF⊥CF(如图2),若AD=2,BC=4,求EF的长.
【答案】(1)、证明过程见解析;(2)、证明过程见解析;(3)、2.
【解析】
试题分析:(1)、根据∠DEC=90°得出∠AED+∠CEB=90°,结合∠ADE+∠AED=90°得出∠ADE=∠CEB,从而说明三角形全等;(2)、根据图形得出△ADE,△DEC,△BEC都是直角三角形,然后根据全等得出BE=a,BC=b,然后根据面积相等的法则得出答案;(3)、根据题意得出△AFD和△BCF相似,设AF=x,则BF=6-x,从而求出x的值,然后得出EF的长度.
试题解析:(1)如图1,∵∠DEC=90°,∴∠AED+∠CEB=90°,∵∠ADE+∠AED=90°,
∴∠ADE=∠CEB,
在△ADE和△BEC中, ,∴△ADE≌△BEC(AAS);
,∴△ADE≌△BEC(AAS);
(2)、如图1,∵AB⊥BC,∠DEC=90°,∴△ADE,△DEC,△BEC都是直角三角形,
∵AD=a,AE=b,DE=c,且DE=EC,△ADE≌△BEC,∴BE=a,BC=b,
∴![]() (a+b)(a+b)=
(a+b)(a+b)=![]() ab+
ab+![]() c2+
c2+![]() ab,
ab,
整理得:a2+b2=c2;
(3)、如图2,由(1)得:△ADE≌△BEC(AAS),则AD=BE=2,BC=AE=4,
∵DF⊥CF, ∴∠AFD+∠BFC=90°,∵∠BFC+∠BCF=90°,∴∠AFD=∠BCF,又∵∠A=∠B,
∴△AFD∽△BCF,∴![]() ,设AF=x,则BF=6﹣x,故
,设AF=x,则BF=6﹣x,故![]() ,
,
解得:x1=2,x2=4, ∵点F不与点E重合, ∴x=2,∴EF=6﹣2﹣2=2.


科目:初中数学 来源: 题型:
【题目】为了解某校八年级720名学生的体重情况,从中抽查了80名学生的体重进行统计分析,以下说法正确的是( )
A.这80名学生是总体的一个样本B.80名学生是样本容量
C.每名学生的体重是个体D.720名学生是总体
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一种面粉的质量标识为“25±0.25千克”,则下列面粉中合格的是( )
A. 24.70千克 B. 25.30千克 C. 24.80千克 D. 25.51千克
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】观察下列算式:
21=2,22=4,23=8,24=16,25=32,26=64, 27=128,28=256,…根据上述算式中的规律,你认为220的末位数字是 .
A | 2 | -4 | 9 | -10 |
B | 3 | 3 | -7 | 9 |
C | 6 | 12 | 63 | 90 |
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我区某学校为了提升学生的体艺素养,准备开设空手道、素描、剪纸三项活动课程,为了解学生对各项活动的兴趣,随机抽取了部分学生进行调查(每人从中必须选取一项,且只能选一项),将调查结果绘制成下面两个统计图,请你结合图中信息解答问题.
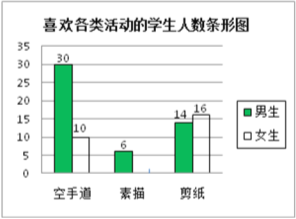

(1)将条形统计图补充完整;
(2)本次抽样调查的样本容量是____________;
(3)已知该校有1200名学生,请你根据样本估计全校学生中喜欢剪纸的人数.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com