
【题目】如图1在正方形ABCD的外侧作两个等边三角形ADE和DCF,连接AF,BE.

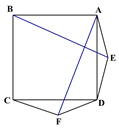

(图1) (图2) (备用图)
(1)请判断:AF与BE的数量关系是_____________,位置关系______________;
(2)如图2,若将条件“两个等边三角形ADE和DCF”变为“两个等腰三角形ADE和DCF,且EA=ED=FD=FC”,第(1)问中的结论是否仍然成立?请作出判断并给予证明;
(3)若三角形ADE和DCF为一般三角形,且AE=DF,ED=FC,第(1)问中的结论都能成立吗?请直接写出你的判断.
【答案】(1)AF=BE,AF⊥BE(2)结论成立(3)结论都能成立
【解析】试题分析:(1)根据正方形和等边三角形可证明△ABE≌△DAF,然后可得BE=AF,∠ABE=∠DAF,进而通过直角可证得BE⊥AF;
(2)类似(1)的证法,证明△ABE≌△DAF,然后可得AF=BE,AF⊥BE,因此结论还成立;
(3)类似(1)(2)证法,先证△AED≌△DFC,然后再证△ABE≌△DAF,因此可得证结论.
试题解析:解:(1)AF=BE,AF⊥BE.
(2)结论成立.
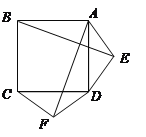
证明:∵四边形ABCD是正方形,
∴BA="AD" =DC,∠BAD =∠ADC = 90°.
在△EAD和△FDC中,
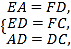
∴△EAD≌△FDC.
∴∠EAD=∠FDC.
∴∠EAD+∠DAB=∠FDC+∠CDA,
即∠BAE=∠ADF.
在△BAE和△ADF中,
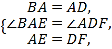
∴△BAE≌△ADF.
∴BE = AF,∠ABE=∠DAF.
∵∠DAF +∠BAF=90°,
∴∠ABE +∠BAF=90°,
∴AF⊥BE.
(3)结论都能成立.


 期末1卷素质教育评估卷系列答案
期末1卷素质教育评估卷系列答案科目:初中数学 来源: 题型:
【题目】已知一次函数y=2x+4
(1)在如图所示的平面直角坐标系中,画出函数的图象;
(2)求图象与x轴的交点A的坐标,与y轴交点B的坐标;
(3)在(2)的条件下,求出△AOB的面积;
(4)利用图象直接写出:当y<0时,x的取值范围.

【答案】(1)画图见解析;(2)A(﹣2,0)B(0,4);(3)4;(4)x<﹣2.
【解析】试题分析:(1)求得一次函数y=2x+4与x轴、y轴的交点坐标,利用两点确定一条直线就可以画出函数图象;(2)由(1)即可得结论;(3)通过交点坐标根据三角形的面积公式即可求出面积;(4)观察函数图象与x轴的交点就可以得出结论.
试题解析:(1)当x=0时y=4,当y=0时,x=﹣2,则图象如图所示

(2)由上题可知A(﹣2,0)B(0,4),
(3)S△AOB=![]() ×2×4=4,
×2×4=4,
(4)x<﹣2.
考点:一次函数图象与系数的关系;一次函数的图象.
【题型】解答题
【结束】
21
【题目】在社会主义新农村建设中,衢州某乡镇决定对A、B两村之间的公路进行改造,并有甲工程队从A村向B村方向修筑,乙工程队从B村向A村方向修筑.已知甲工程队先施工3天,乙工程队再开始施工.乙工程队施工几天后因另有任务提前离开,余下的任务有甲工程队单独完成,直到公路修通.下图是甲乙两个工程队修公路的长度y(米)与施工时间x(天)之间的函数图象,请根据图象所提供的信息解答下列问题:

(1)乙工程队每天修公路多少米?
(2)分别求甲、乙工程队修公路的长度y(米)与施工时间x(天)之间的函数关系式.
(3)若该项工程由甲、乙两工程队一直合作施工,需几天完成?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商品的批发价为a元,先提高10%零售,后又按零售价降低10%出售,则它最后的单价是( )元.
A.a
B.0.99a
C.1.21a
D.0.81a
查看答案和解析>>
科目:初中数学 来源: 题型:
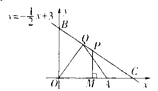
【题目】如图,点A的坐标为(4,0).点P是直线y=![]()
![]() x+3在第一象限内的点,过P作PM
x+3在第一象限内的点,过P作PM![]() x轴于点M,O是原点.
x轴于点M,O是原点.
(1)设点P的坐标为(x, y),试用它的纵坐标y表示△OPA的面积S;
(2)S与y是怎样的函数关系?它的自变量y的取值范围是什么?
(3)如果用P的坐标表示△OPA的面积S,S与x是怎样的函数关系?它的自变量的取值范围是什么?
(4)在直线y=![]()
![]() x+3上求一点Q,使△QOA是以OA为底的等腰三角形.
x+3上求一点Q,使△QOA是以OA为底的等腰三角形.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com