练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】解方程

    （1）＝x﹣2；

    （2）＝2

    【答案】（1）x＝3；（2）x＝1

    【解析】

    （1）依次去分母，去括号，移项，合并同类项，系数化为1，即可得到答案，

    （2）先把方程进行整理，然后去分母，去括号，移项，合并同类项，系数化为1，即可得到答案．

    （1）去分母得：2（2x﹣1）﹣（x+1）＝6（x﹣2），

    去括号得：4x﹣2﹣x﹣1＝6x﹣12，

    移项得：4x﹣x﹣6x＝﹣12+2+1，

    合并同类项得：﹣3x＝﹣9，

    系数化为1得：x＝3，

    （2）原方程可整理得：，

    去分母得：5（10x+10）﹣2（10x+30）＝20，

    去括号得：50x+50﹣20x﹣60＝20，

    移项得：50x﹣20x＝20+60﹣50，

    合并同类项得：30x＝30，

    系数化为1得：x＝1．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】已知：如图，AB是⊙O的直径，弦 ，∠B=60°，OD⊥AC，垂足为D．

    （1）求OD的长；
    （2）求劣弧AC的长．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图1所示，从边长为a的正方形纸片中减去一个边长为b的小正方形，再沿着线段AB剪开，把剪成的两张纸拼成如图2的等腰梯形（其面积= ）.

    （1）设图1中阴影部分面积为S1，图2中阴影部分面积为S2，请直接用含a、b的式子表示S1和S2；

    （2）请写出上述过程所揭示的乘法公式．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，在平面直角坐标中，点的坐标为，点的坐标为，将线段向右平移个单位长度得到线段（点和点分别是点和点的对应点），连接、，点是线段的中点.

    备用图

    （1）求点的坐标；

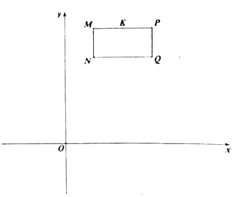
    （2）若长方形以每秒个单位长度的速度向正下方运动，（点、、、、分别是点、、、、的对应点），当与轴重合时停止运动，连接、，设运动时间为妙，请用含的式子表示三角形的面积（不要求写出的取值范围）；

    （3）在（2）的条件下，连接、，问是否存在某一时刻，使三角形的面积等于三角形的面积？若存在，请求出值；若不存在，请说明理由.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】在平面直角坐标系xOy中，⊙O的半径为1，P是坐标系内任意一点，点P到⊙O的距离SP的定义如下：若点P与圆心O重合，则SP为⊙O的半径长；若点P与圆心O不重合，作射线OP交⊙O于点A，则SP为线段AP的长度．
    图1为点P在⊙O外的情形示意图．

    （1）若点B（1，0），C（1，1），D(0， )，则SB=；SC=；SD=；
    （2）若直线y=x+b上存在点M，使得SM=2，求b的取值范围；
    （3）已知点P，Q在x轴上，R为线段PQ上任意一点．若线段PQ上存在一点T，满足T在⊙O内且ST≥SR ， 直接写出满足条件的线段PQ长度的最大值．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，点A（6，3）、B（6，0）在直角坐标系内．以原点O为位似中心，相似比为 ，在第一象限内把线段AB缩小后得到线段CD，那么点C的坐标为（ ）

    A.（3，1）
    B.（2，0）
    C.（3，3）
    D.（2，1）

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，在平面直角坐标系xOy中，一次函数y=﹣2x的图象与反比例函数y= 的图象交于点A（﹣1，n）．

    （1）求反比例函数y= 的解析式；
    （2）若P是坐标轴上一点，且满足PA=OA，直接写出点P的坐标．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】在平面直角坐标系xOy中，对于点P（x，y）和Q（x，y′），给出如下定义：
    如果y′= ，那么称点Q为点P的“关联点”．
    例如：点（5，6）的“关联点”为点（5，6），点（﹣5，6）的“关联点”
    为点（﹣5，﹣6）．
    （1）①点（2，1）的“关联点”为；②如果点A（3，﹣1），B（﹣1，3）的“关联点”中有一个在函数 的图象上，那么这个点是（填“点A”或“点B”）．
    （2）①如果点M*（﹣1，﹣2）是一次函数y=x+3图象上点M的“关联点”，
    那么点M的坐标为；②如果点N*（m+1，2）是一次函数y=x+3图象上点N的“关联点”，求点N的坐标 ．
    （3）如果点P在函数y=﹣x2+4（﹣2＜x≤a）的图象上，其“关联点”Q的纵坐标
    y′的取值范围是﹣4＜y′≤4，那么实数a的取值范围是 ．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】国家规定个人发表文章、出版图书所得稿费的纳税计算方法是：

    ①稿费不高于800元的不纳税；

    ②稿费高于800元，而低于4000元的应缴纳超过800元的那部分稿费的14%的税；

    ③稿费为4000元或高于4000元的应缴纳全部稿费的11%的税．

    试根据上述纳税的计算方法作答：

    （1）若王老师获得的稿费为2400元，则应纳税 元，若王老师获得的稿费为4000元，则应纳税 元；

    （2）若王老师获稿费后纳税420元，求这笔稿费是多少元？

    查看答案和解析>>

    同步练习册答案