
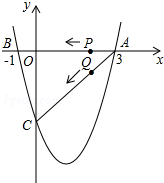
 如图,二次函数y=$\frac{4}{3}$x2+bx+c的图象与x轴交于A(3,0),B(-1,0),与y轴交于点C.若点P,Q同时从A点出发,都以每秒1个单位长度的速度分别沿AB,AC边运动,其中一点到达端点时,另一点也随之停止运动.
如图,二次函数y=$\frac{4}{3}$x2+bx+c的图象与x轴交于A(3,0),B(-1,0),与y轴交于点C.若点P,Q同时从A点出发,都以每秒1个单位长度的速度分别沿AB,AC边运动,其中一点到达端点时,另一点也随之停止运动.分析 (1)将A,B点坐标代入函数y=$\frac{4}{3}$x2+bx+c中,求得b、c,进而可求解析式及C坐标;
(2)等腰三角形有三种情况,AE=EQ,AQ=EQ,AE=AQ.借助垂直平分线,画圆易得E大致位置,设边长为x,表示其它边后利用勾股定理易得E坐标;
(3)注意到P,Q运动速度相同,则△APQ运动时都为等腰三角形,又由A、D对称,则AP=DP,AQ=DQ,易得四边形四边都相等,即菱形.利用菱形对边平行且相等的性质可用t表示D点坐标,又D在E函数上,所以代入即可求t,进而D可表示;
(4)求出直线AC的解析式yAC=$\frac{4}{3}x-4$,W=yAC-y=$\frac{4}{3}x-4$-($\frac{4}{3}$x2-$\frac{8}{3}$x-4)=-$\frac{4}{3}$x2+4x,求出对称轴x=$\frac{3}{2}$,代入y=$\frac{4}{3}$x2-$\frac{8}{3}$x-4=-5,所以R($\frac{3}{2}$,-5).
解答 解:(1)∵二次函数y=$\frac{4}{3}$x2+bx+c的图象与x轴交于A(3,0),B(-1,0),
∴$\left\{\begin{array}{l}{\frac{4}{3}×9+3b+c=0}\\{\frac{4}{3}×1-b+c=0}\end{array}\right.$,
解得$\left\{\begin{array}{l}{b=-\frac{8}{3}}\\{c=-4}\end{array}\right.$,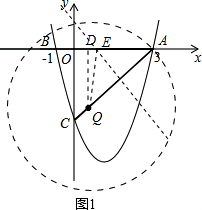
∴y=$\frac{4}{3}$x2-$\frac{8}{3}$x-4,
∴C(0,-4).
(2)存在.
如图1,过点Q作QD⊥OA于D,此时QD∥OC
∵A(3,0),B(-1,0),C(0,-4),O(0,0)
∴AB=4,OA=3,OC=4,
∴AC=$\sqrt{{3}^{2}+{4}^{2}}$=5,AQ=4.
∵QD∥OC,
∴$\frac{QD}{OC}=\frac{AD}{AO}=\frac{AQ}{AC}$,
∴$\frac{QD}{4}=\frac{AD}{3}=\frac{4}{5}$,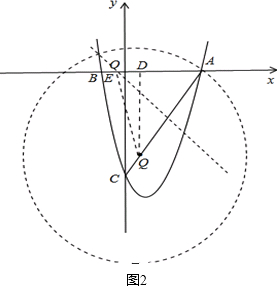
∴QD=$\frac{16}{5}$,AD=$\frac{12}{5}$.
①作AQ的垂直平分线,交AO于E,此时AE=EQ,即△AEQ为等腰三角形
设AE=x,则EQ=x,DE=AD-AE=$\frac{12}{5}$-x,
∴在Rt△EDQ中,($\frac{12}{5}$-x)2+($\frac{16}{5}$)2=x2,解得 x=$\frac{10}{3}$,
∴OA-AE=3-$\frac{10}{3}$=-$\frac{1}{3}$,
∴E(-$\frac{1}{3}$,0).
②以Q为圆心,AQ长半径画圆,交x轴于E,此时QE=QA=4,
∵ED=AD=$\frac{12}{5}$,
∴AE=$\frac{24}{5}$,
∴OA-AE=3-$\frac{24}{5}$=-$\frac{9}{5}$,
∴E(-$\frac{9}{5}$,0).
③当AE=AQ=4时,
∵OA-AE=3-4=-1,或OA+AE=7
∴E(-1,0)或(7,0).
综上所述,存在满足条件的点E,点E的坐标为(-$\frac{1}{3}$,0)或(-$\frac{9}{5}$,0)或(-1,0)或(7,0).
(3)四边形APDQ为菱形,D点坐标为(-$\frac{5}{8}$,-$\frac{29}{16}$).理由如下: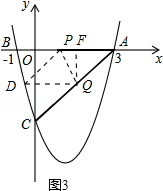
如图3,D点关于PQ与A点对称,过点Q作,FQ⊥AP于F,
∵AP=AQ=t,AP=DP,AQ=DQ
∴AP=AQ=QD=DP,
∴四边形AQDP为菱形,
∵FQ∥OC,
∴$\frac{AF}{AO}=\frac{FQ}{OC}=\frac{AQ}{AC}$,
∴$\frac{AF}{3}=\frac{FQ}{4}=\frac{t}{5}$
∴AF=$\frac{3}{5}t$,FQ=$\frac{4}{5}t$•
∴Q(3-$\frac{3}{5}t$,-$\frac{4}{5}t$),
∵DQ=AP=t,5
∴D(3-$\frac{3}{5}t$-t,-$\frac{4}{5}t$),
∵D在二次函数y=$\frac{4}{3}$x2-$\frac{8}{3}$x-4上,
∴-$\frac{4}{5}t$=$\frac{4}{3}$(3-$\frac{8}{5}$t)2-$\frac{8}{3}$(3-$\frac{8}{5}$t)-4,
∴t=$\frac{145}{64}$,或t=0(与A重合,舍去),
∴D(-$\frac{5}{8}$,-$\frac{29}{16}$).
(4)R($\frac{3}{2}$,-5).
∵A(3,0),C(0,-4),
∴yAC=$\frac{4}{3}x-4$,
设RM=W,
则W=yAC-y=$\frac{4}{3}x-4$-($\frac{4}{3}$x2-$\frac{8}{3}$x-4)=-$\frac{4}{3}$x2+4x,
对称轴为:x=$\frac{3}{2}$,
把x=$\frac{3}{2}$代入y=$\frac{4}{3}$x2-$\frac{8}{3}$x-4=-5,
所以R($\frac{3}{2}$,-5).
点评 本题考查了二次函数性质、利用勾股定理解直角三角形及菱形等知识,总体来说题意复杂但解答内容都很基础,是一道值得练习的题目,熟练地运用数形结合是解决问题的关键.


科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,点M,N分别是正五边形ABCDE的边BC,CD上的点,且BM=CN,AM交BN于点P.
如图,点M,N分别是正五边形ABCDE的边BC,CD上的点,且BM=CN,AM交BN于点P.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
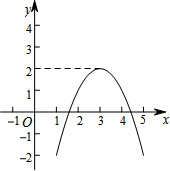 对某一个函数给出如下定义:如果存在实数M,对于任意的函数值y,都满足y≤M,那么称这个函数是有上界函数,在所有满足条件的M中,其最小值称为这个函数的上确界.例如,图中的函数是有上界函数,其上确界是2.
对某一个函数给出如下定义:如果存在实数M,对于任意的函数值y,都满足y≤M,那么称这个函数是有上界函数,在所有满足条件的M中,其最小值称为这个函数的上确界.例如,图中的函数是有上界函数,其上确界是2.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
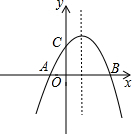 如图,已知二次函数y=-(x+1)(x-m)的图象与x轴相交于点A、B(点A在点B的左侧),与y轴相交于点C,且图象经过点M(2,3).
如图,已知二次函数y=-(x+1)(x-m)的图象与x轴相交于点A、B(点A在点B的左侧),与y轴相交于点C,且图象经过点M(2,3).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,某校综合实践活动小组的同学欲测量公园内一棵树DE的高度,他们在这棵树正前方一座楼亭前的台阶上A点处测得树顶端D的仰角为30°,朝着这棵树的方向走到台阶下的点C处,测得树顶端D的仰角为60°.已知A点的高度AB为2m,台阶AC的坡度为1:$\sqrt{3}$,且B、C、E三点在同一条直线上.请根据以上条件:
如图,某校综合实践活动小组的同学欲测量公园内一棵树DE的高度,他们在这棵树正前方一座楼亭前的台阶上A点处测得树顶端D的仰角为30°,朝着这棵树的方向走到台阶下的点C处,测得树顶端D的仰角为60°.已知A点的高度AB为2m,台阶AC的坡度为1:$\sqrt{3}$,且B、C、E三点在同一条直线上.请根据以上条件:查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,在?ABCD中,BC=10,sinB=$\frac{9}{10}$,AC=BC,则?ABCD的面积是( )
如图,在?ABCD中,BC=10,sinB=$\frac{9}{10}$,AC=BC,则?ABCD的面积是( )| A. | 2$\sqrt{19}$ | B. | 6$\sqrt{19}$ | C. | 9$\sqrt{19}$ | D. | 18$\sqrt{19}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com