
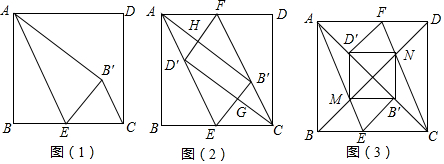
分析 (1)问题1:欲证明B′C∥AE,只要证明∠AEB′=∠EB′C即可;
问题2:根据三个角是直角的四边形是矩形即可判断;
(2)利用全等三角形的性质只要证明OM=OB′=ON=OD′,NM⊥B′D′即可.
解答 (1)问题1:证明:如图1中,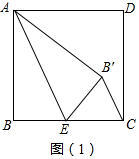
∵△ABE和△AB′E关于AE对称,
∴∠AEB=∠AEB′,BE=B′E,
∵BE=EC,
∴B′E=EC,
∴∠EB′C=∠ECB′,
∵∠BEB′=∠EB′C+∠ECB′,
∴∠AEB=∠B′CE,
∴AE∥B′C,
问题2:证明:如图2中,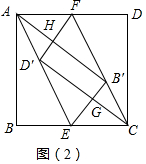
∵四边形ABCD是正方形,
∴AB=BC=CD=AD,∠BAD=∠B=∠BCD=∠D=90°,
∵BE=DF,
∴△ABE≌△CDF,
∴∠BAE=∠DCF,
∵∠BAE=∠B′AE,∠DCF=∠D′CF,
∴∠BAB′=∠DCD′,
∵∠D=∠D′=90°,
∴∠D′FD+∠D′CD=180°,
∵∠AFD′+∠D′FD=180°,
∴∠AFD′=∠D′CD=∠BAB′,
∵∠B′AD+∠BAB′=90°,
∴∠AFD′+∠B′AF=90°,
∴∠AHF=∠B′HD′=90°,
∴四边形D′DB′H是矩形.
(2)拓展探究:实践小组的同学们发现的结论是正确的.
证明:如图3中,连接BB′、DD′,则BB′⊥AE,DD′⊥CF.
∵四边形ABCD是正方形,
∴OA=OB=OC=OD,AC⊥BD,
∴∠MAO+∠AMO=90°,∠OBB′+∠BME=90°,
∵∠AMO=∠BME,
∴∠MAO=∠OB′B,
∴△AMO≌△BB′O,
∴OM=OB′,同理ON=OD′,
∵∠BAM=∠DCN,∠ABM=∠CDN,AB=CD,
∴△BAM≌△DCN,
∴MB=DN.
∴OM=ON,
∴OM=OB′=ON=OD′,
∴四边形MB′ND′是矩形,
∴AC⊥BD,
∴四边形MB′ND′是正方形.
点评 本题考查四边形综合题、全等三角形的判定和性质、正方形的性质和判定、矩形的判定和性质等知识,解题的关键是正确寻找全等三角形解决问题,灵活运用所学知识解决问题,属于中考压轴题.


 课前课后同步练习系列答案
课前课后同步练习系列答案 课堂小作业系列答案
课堂小作业系列答案 黄冈小状元口算速算练习册系列答案
黄冈小状元口算速算练习册系列答案 成功训练计划系列答案
成功训练计划系列答案 倍速训练法直通中考考点系列答案
倍速训练法直通中考考点系列答案 一卷搞定系列答案
一卷搞定系列答案科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:填空题
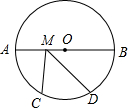 如图,⊙O的半径是8,AB是⊙O的直径,M为AB上一动点,$\widehat{AC}$=$\widehat{CD}$=$\widehat{BD}$,则CM+DM的最小值为16.
如图,⊙O的半径是8,AB是⊙O的直径,M为AB上一动点,$\widehat{AC}$=$\widehat{CD}$=$\widehat{BD}$,则CM+DM的最小值为16.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,在平面直角坐标系中,已知抛物线y=ax2+bx-2(a≠0)与x轴交于A(1,0),B(3,0)两点,与y轴交于点C,其顶点为点D,点E的坐标为(0,-1),该抛物线与BE交于另一点F,连接BC.
如图,在平面直角坐标系中,已知抛物线y=ax2+bx-2(a≠0)与x轴交于A(1,0),B(3,0)两点,与y轴交于点C,其顶点为点D,点E的坐标为(0,-1),该抛物线与BE交于另一点F,连接BC.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
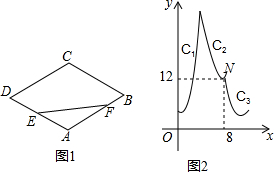 如图1,在菱形ABCD中,点E为AD的中点,点F为折线A-B-C-D上一个动点(从点A出发到点D停止),连结EF,设点F的运动路径的长为x,EF2为y,y关于x的函数图象由C1,C2,C3三段组成,已知C2与C3的界点N的坐标如图2所示.
如图1,在菱形ABCD中,点E为AD的中点,点F为折线A-B-C-D上一个动点(从点A出发到点D停止),连结EF,设点F的运动路径的长为x,EF2为y,y关于x的函数图象由C1,C2,C3三段组成,已知C2与C3的界点N的坐标如图2所示.查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com