
分析 因为k=-5<0,b=-3<0,根据一次函数y=kx+b(k≠0)的性质得到图象经过第二、四象限,图象与y轴的交点在x轴下方,于是可判断一次函数y=-5x-3的图象经过第二、三、四象限.
解答 解:对于一次函数y=-5x-3,
∵k=-5<0,
∴图象经过第二、四象限;
又∵b=-3<0,
∴一次函数的图象与y轴的交点在x轴下方,即函数图象还经过第三象限,
∴一次函数y=-5x-3的图象经过第二、三、四象限.
故答案为:二、三、四.
点评 本题考查了一次函数y=kx+b(k≠0)的性质:当k<0,图象经过第二、四象限,y随x的增大而减小;当k>0,经图象第一、三象限,y随x的增大而增大;当b>0,一次函数的图象与y轴的交点在x轴上方;当b<0,一次函数的图象与y轴的交点在x轴下方.


 星级口算天天练系列答案
星级口算天天练系列答案科目:初中数学 来源: 题型:选择题
| A. | $\frac{1}{2}$ | B. | $\frac{1}{3}$ | C. | $\frac{1}{4}$ | D. | $\frac{1}{6}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 北京时间2015年04月25日14时11分,尼泊尔发生8.1级强烈地震,我国积极组织抢险队赴地震灾区参与抢险工作.如图,某探测队在地面A、B两处均探测出建筑物下方C处有生命迹象,已知探测线与地面的夹角分别是25°和60°,且AB=4米,求该生命迹象所在位置C的深度.(结果精确到1米.参考数据:sin25°≈0.4,cos25°≈0.9,tan25°≈0.5,$\sqrt{3}$≈1.7)
北京时间2015年04月25日14时11分,尼泊尔发生8.1级强烈地震,我国积极组织抢险队赴地震灾区参与抢险工作.如图,某探测队在地面A、B两处均探测出建筑物下方C处有生命迹象,已知探测线与地面的夹角分别是25°和60°,且AB=4米,求该生命迹象所在位置C的深度.(结果精确到1米.参考数据:sin25°≈0.4,cos25°≈0.9,tan25°≈0.5,$\sqrt{3}$≈1.7)查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\sqrt{13}+\sqrt{3}=\sqrt{16}=4$ | B. | $\sqrt{121÷4}=\sqrt{121}÷\sqrt{4}=\frac{11}{2}$ | C. | $3+\sqrt{3}=3\sqrt{3}$ | D. | $\sqrt{4\frac{1}{3}}=2\sqrt{\frac{1}{3}}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
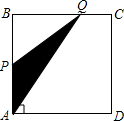 如图,四边形ABCD是矩形,AB=8,BC=4,动点P以每秒2个单位的速度从点A沿线段AB向B点运动,同时动点Q以每秒3个单位的速度从点B出发沿B-C-D的方向运动,当点Q到达点D时P、Q同时停止运动,若记△PQA的面积为y,运动时间为x,则下列图象中能大致表示y与x之间函数关系图象的是( )
如图,四边形ABCD是矩形,AB=8,BC=4,动点P以每秒2个单位的速度从点A沿线段AB向B点运动,同时动点Q以每秒3个单位的速度从点B出发沿B-C-D的方向运动,当点Q到达点D时P、Q同时停止运动,若记△PQA的面积为y,运动时间为x,则下列图象中能大致表示y与x之间函数关系图象的是( )| A. | 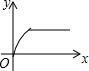 | B. | 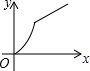 | C. |  | D. |  |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com