
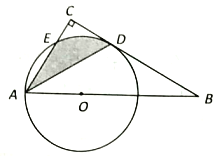
【题目】如图,点0 为Rt△ABC斜边AB上的一点,以OA 为半径的☉O与BC切于点D,与AC 交于点E,连接AD.
(1) 求证: AD平分∠BAC;
(2)若∠BAC= 60°,OA=4,求阴影部分的面积(结果保留π).
【答案】(1)见解析;(2)![]()
【解析】试题分析:
(1)连接OD,则由已知易证OD∥AC,从而可得∠CAD=∠ODA,结合∠ODA=∠OAD,即可得到∠CAD=∠OAD,从而得到AD平分∠BAC;
(2)连接OE、DE,由已知易证△AOE是等边三角形,由此可得∠ADE=![]() ∠AOE=30°,由AD平分∠BAC可得∠OAD=30°,从而可得∠ADE=∠OAD,由此可得DE∥AO,从而可得S阴影=S扇形ODE,这样只需根据已知条件求出扇形ODE的面积即可.
∠AOE=30°,由AD平分∠BAC可得∠OAD=30°,从而可得∠ADE=∠OAD,由此可得DE∥AO,从而可得S阴影=S扇形ODE,这样只需根据已知条件求出扇形ODE的面积即可.
试题解析:
(1)连接OD.
∵BC是⊙O的切线,D为切点,
∴OD⊥BC.
又∵AC⊥BC,
∴OD∥AC,
∴∠ADO=∠CAD.
又∵OD=OA,
∴∠ADO=∠OAD,
∴∠CAD=∠OAD,即AD平分∠BAC.
(2)连接OE,ED.
∵∠BAC=60°,OE=OA,
∴△OAE为等边三角形,
∴∠AOE=60°,
∴∠ADE=30°.
又∵![]() ,
,
∴∠ADE=∠OAD,
∴ED∥AO,
∴S△AED=S△OED,
∴阴影部分的面积 = S扇形ODE = ![]() .
.



科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD内接于⊙O,BC是直径,∠BAD=120°,AB=AD.
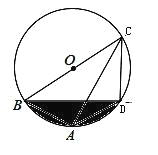
(1)求证:四边形ABCD是等腰梯形;
(2)已知AC=6,求阴影部分的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,两幢建筑物AB和CD,AB⊥BD,CD⊥BD,AB=15m,CD=20m,AB和CD之间有一观景池,小南在A点测得池中喷泉处E点的俯角为42°,在C点测得E点的俯角为45°(点B、E、D在同一直线上),求两幢建筑物之间的距离BD.(结果精确到0.1m).

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】东营市某中学校团委开展“关爱残疾儿童”爱心捐书活动,全校师生踊跃捐赠各类书籍共3000本.为了了解各类书籍的分布情况,从中随机抽取了部分书籍分四类进行统计:A.艺术类;B.文学类;C.科普类;D.其他,并将统计结果绘制成如图所示的两幅不完整的统计图.
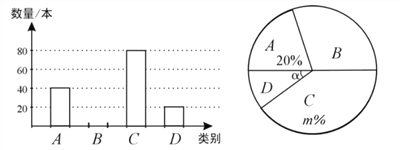
(1)这次统计共抽取_____本书籍,扇形统计图中的m=______,∠α的度数是_____
(2)请将条形统计图补充完整;
(3)估计全校师生共捐赠了多少本文学类书籍.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,有一Rt△ABC,∠C=90°且A(-1,3)、B(-3,-1)、C(-3,3),已知△A1AC1是由△ABC旋转得到的.若点Q在x轴上,点P在直线AB上,要使以Q、P、A1、C1为顶点的四边形是平行四边形,满足条件的点Q的坐标为______.
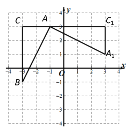
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,已知∠ABC=![]() ,D是直线AB上的一点,AD=BC,连结DC.以DC为边,在∠CDB的同侧作∠CDE,使得∠CDE=∠ABC,并截取DE=CD,连结AE.
,D是直线AB上的一点,AD=BC,连结DC.以DC为边,在∠CDB的同侧作∠CDE,使得∠CDE=∠ABC,并截取DE=CD,连结AE.
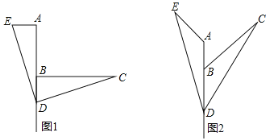
(1)求证:![]() ;并判断AE和BC的位置关系,说明理由;
;并判断AE和BC的位置关系,说明理由;
(2)若将题目中的条件“∠ABC=900”改成“∠ABC=x0(0<x<180)”,
①结论“![]() ”还成立吗?请说明理由;②试探索:当
”还成立吗?请说明理由;②试探索:当![]() 的值为多少时,直线AE⊥BC.
的值为多少时,直线AE⊥BC.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数y=x2﹣3x+m(m为常数)的图象与x轴的一个交点为(1,0),则关于x的一元二次方程x2﹣3x+m=0的两实数根是( )
A. x1=1,x2=﹣1 B. x1=1,x2=2 C. x1=1,x2=0 D. x1=1,x2=3
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知点 A(-5,0)、B(3,0).
(1)若点 C 在 y 轴上,且使得△ABC 的面积等于 16,求点 C 的坐标;
(2)若点 C 在坐标平面内,且使得△ABC 的面积等于 16,这样的点 C 有多少个?你发 现了什么规律?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com