练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    18．一次函数y=kx+6的图象经过一、二、四象限，则k的取值范围为k＜0．

    分析 根据一次函数y=kx+6的图象经过一、二、四象限可直接得出结论．

    解答 解：∵一次函数y=kx+6的图象经过一、二、四象限，
    ∴k＜0．
    故答案为：k＜0．

    点评 本题考查的是一次函数的性质，熟知一次函数y=kx+b（k≠0）中，当k＜0，b＞0时，函数的图象经过一、二、四象限是解答此题的关键．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：选择题

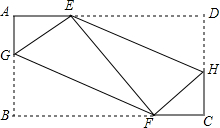    7．已知在矩形ABCD中，AB=4，AD=7，点G、F、H、E是分别边AB、BC、DC、AD上的点，分别沿HE，GF折叠矩形恰好使DE、BF都与EF重合，则AE=（　　）
    A．1或$\frac{8}{3}$B．2或$\frac{8}{3}$C．$\frac{3}{2}$或$\frac{8}{3}$D．$\frac{5}{2}$或$\frac{8}{3}$

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    9．已知m是方程x2=x+1的一个根，则关于x的方程x2+2xm2-2xm-1=0有一个根是（　　）
    A．$\sqrt{2}$B．-$\sqrt{2}$C．-1+$\sqrt{2}$D．1-$\sqrt{2}$

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

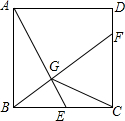    6．如图，已知正方形ABCD的边长为2，E是BC边上的动点，BF⊥AE交CD于点F，垂足为G，连结CG．则CG的最小值为$\sqrt{5}$-1．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    13．设直线y=ax+b与抛物线y=x2的交点A，B的横坐标分别为3，-1．
    （1）求a，b的值；
    （2）设抛物线的顶点为C，求△ABC的面积．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    3．设计一个商标图案如图中阴影部分所示，长方形ABCD中，AB=a，BC=b，以点A为圆心，AD为半径作圆弧与BA的延长线相交于点F，求商标图案的面积．（其中a=4，b=2）．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    10．请你任意写出一个经过（0，3）点，且y随x的增大而减小的一次函数的解析式y=-x+3（答案不唯一）．（写出一种即可）

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    7．在平面直角坐标系xOy中，对于点P（x，y）和Q（x，y′），给出如下定义：
    如果y′=$\left\{\begin{array}{l}{y（x≥0）}\\{-y（x＜0）}\end{array}\right.$，那么称点Q为点P的“妫川伴侣”．
    例如：点（5，6）的“妫川伴侣”为点（5，6），点（-5，6）的“妫川伴侣”为点（-5，-6）．
    （1）①点（2，1）的“妫川伴侣”为（2，1）；
    ②如果点A（3，-1），B（-1，3）的“妫川伴侣”中有一个在函数$y=\frac{3}{x}$的图象上，那么这个点是B（填“点A”或“点B”）．
    （2）①点M*（-1，-2）的“妫川伴侣”点M的坐标为（-1，2）；
    ②如果点N*（m+1，2）是一次函数y=x+3图象上点N的“妫川伴侣”，
    求点N的坐标．
    （3）如果点P在函数y=-x2+4（-2＜x≤a）的图象上，其“妫川伴侣”Q的纵坐标y′的取值范围是-4＜y′≤4，那么实数a的取值范围是2≤a＜2$\sqrt{2}$．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    8．$\frac{1}{3}$，$\sqrt{3}$，π，$\sqrt{25}$中无理数有（　　）
    A．1个B．2个C．3个D．4个

    查看答案和解析>>

    同步练习册答案