
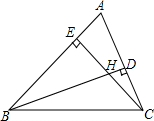
 如图,在△ABC中,BD、CE分别是AC、AB边上的高,H是BD、CE的交点,试猜想∠A和∠EHD之间的数量关系,并证明你的猜想.
如图,在△ABC中,BD、CE分别是AC、AB边上的高,H是BD、CE的交点,试猜想∠A和∠EHD之间的数量关系,并证明你的猜想. 分析 由于∠DHE是△BEH的外角,故∠DHE=∠HBE+∠BEH=∠HBE+90°=∠HBE+∠ADB,即∠A+∠EHD=∠HBE+∠ADB+∠A=180°.
解答 解:∠A+∠EHD=180°.
∵BD,CE是△ABC的高(已知),
∴∠BEH=∠ADB=90°(高的意义),
∵∠DHE是△BEH的外角(三角形外角的概念),
∴∠DHE=∠HBE+∠BEH(三角形的一个外角等于不相邻的两个内角的和),
=∠HBE+90°
=∠HBE+∠ADB,
∴∠A+∠DHE=∠A+∠HBE+∠ADB=90°+90°=180°.
点评 本题考查了三角形内角和定理,此类题目比较简单,解答此类题目要注意:①求角的度数常常要用到“三角形的内角和是180°这一隐含的条件;②三角形的外角通常情况下是转化为内角来解决.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,在平面直角坐标系中,边长不等的正方形依次排列,每个正方形都有一个顶点落在函数y=$\frac{1}{2}$x的图象上,从左向右第3个正方形中的一个顶点A的坐标为(6,2),阴影三角形部分的面积从左向右依次记为S1、S2、S3、…、Sn,则第4个正方形的边长是3,S3的值为$\frac{81}{8}$.
如图,在平面直角坐标系中,边长不等的正方形依次排列,每个正方形都有一个顶点落在函数y=$\frac{1}{2}$x的图象上,从左向右第3个正方形中的一个顶点A的坐标为(6,2),阴影三角形部分的面积从左向右依次记为S1、S2、S3、…、Sn,则第4个正方形的边长是3,S3的值为$\frac{81}{8}$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,已知Q点的坐标为(-3,0),将点Q向上平移一个单位长度,再向右平移5个单位长度,得到点P.
如图,已知Q点的坐标为(-3,0),将点Q向上平移一个单位长度,再向右平移5个单位长度,得到点P.查看答案和解析>>
科目:初中数学 来源:2017届福建省仙游县郊尾、枫亭五校教研小片区九年级下学期第一次月考数学试卷(解析版) 题型:填空题
若关于 的一元二次方程
的一元二次方程 有两个不相等的实数根,则
有两个不相等的实数根,则 的取值范围是__________.
的取值范围是__________.
查看答案和解析>>
科目:初中数学 来源:2016-2017学年度海南省九年级第二次月考数学试卷(解析版) 题型:解答题
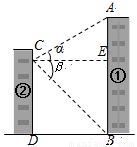
(8分)某中学九年级学生在学习“直角三角形的边角关系”时,组织开展测量物体高度的实践活动.在活动中,某小组为了测量校园内①号楼AB的高度(如图),站在②号楼的C处,测得①号楼顶部A的仰角α=30°,底部B的俯角β=45°.已知两幢楼的水平距离BD为18米,求①号楼AB的高度.(结果保留根号)
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com