
���� ��1���ٸ����������ϵ���ص��Τ�ﶨ�������BC���ڸ���y���ϵ���ص㣬��x=0���y���ɣ�
��2�����������ߵõ���AEM�ס�MCF���ٷ���������ٵ���M��AC�Ϸ�ʱ���������������ACM=30��ʱ�͢���CAM=30�㣬�ڵ���M��AC�·�ʱ���͢�һ����������������ۼ��㣬
��3�������P��m��-$\frac{1}{4}$m2+$\frac{3}{2}$m+4�����õ�Q��m��-$\frac{1}{2}$m+4����������������ۼ��㣮
��� �⣺��1���١߶��κ���y=ax2-6ax-16a��a��0����x�ύ��B��C���㣬
��y=0����ax2-6ax-16a=0��
��BC=|x1-x2|=10��
�ʴ�Ϊ10��
����x=0����y=-16a
��A��0��-16a��
�ʴ�Ϊ��0��-16a����
��2���ߡ�AMC=90��
����ͼ��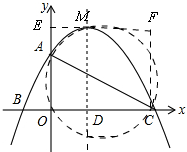
����M��AC�Ϸ�ʱ������M��ֱ��ME��x�ᣬ����C��ֱ��CF��y�ύME�ڵ�F��
��OA=-16a��ME=3��FM=5����AEM�ס�MCF
������ACM=30��ʱ��tan30��=$\frac{AM}{MC}=\frac{\sqrt{3}}{3}$��
�ߡ�AEM�ס�MCF��
��$\frac{AE}{5}=\frac{3}{CF}=\frac{AM}{CM}=\frac{\sqrt{3}}{3}$��
��AE=$\frac{5\sqrt{3}}{3}$��CF=3$\sqrt{3}$��
��OE=CF��
��-16a+$\frac{5\sqrt{3}}{3}$=3$\sqrt{3}$��
��a=-$\frac{\sqrt{3}}{12}$��
������CAM=30��ʱ��cot30��=$\frac{AM}{MC}$=$\sqrt{3}$��
�ߡ�AEM�ס�MCF��
��$\frac{AE}{5}$=$\frac{3}{CF}$=$\frac{AM}{MC}$=$\sqrt{3}$��
��AE=5$\sqrt{3}$��CF=$\sqrt{3}$��
��AE��CF��
����ͼ������AE��CFì�ܣ�����������������ڣ�
����ͼ��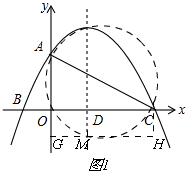
����M��AC�·�ʱ������M��ֱ��MG��x�ᣬ����C��ֱ��CH��y�ύMG�ڵ�H����OA=-16a��MG=3��MH=5����AGM�ס�MHC
������MAC=30��ʱ��cot30��=$\frac{AM}{MC}$=$\sqrt{3}$��
�ߡ�AGM�ס�MHC��
��$\frac{AG}{5}$=$\frac{3}{CH}$=$\frac{AM}{MC}$=$\sqrt{3}$��
��AG=5$\sqrt{3}$��CH=$\sqrt{3}$��
��OG=CH��
��5$\sqrt{3}$-��-16a��=$\sqrt{3}$��
��a=-$\frac{\sqrt{3}}{4}$
������ACM=30��ʱ��tan30��=$\frac{AM}{MC}$=$\frac{\sqrt{3}}{3}$��
�ߡ�AGM�ס�MHC��
��$\frac{AG}{5}$=$\frac{3}{CH}$=$\frac{AM}{MC}$=$\frac{\sqrt{3}}{3}$��
��AG=$\frac{5\sqrt{3}}{3}$��CH=3$\sqrt{3}$
��AG��CH������ͼ������AG��CHì�ܣ�����������������ڣ�
��a��ֵΪ-$\frac{\sqrt{3}}{12}$��-$\frac{\sqrt{3}}{4}$��
��3����a=-$\frac{1}{4}$��
��y=-$\frac{1}{4}$x2+$\frac{3}{2}$x+4��
��A��0��4����C��8��0����
��ֱ��AC��Ӧ�ĺ�����ϵʽΪy=-$\frac{1}{2}$x+4��
��ͼ��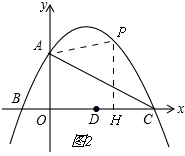
��P��PH��OC������ΪH����ֱ��AC�ڵ�Q��
��P��m��-$\frac{1}{4}$m2+$\frac{3}{2}$m+4������Q��m��-$\frac{1}{2}$m+4����
�ٵ�-2��m��0ʱ����P��x���Ϸ�����ֻһ������
PQ=��-$\frac{1}{2}$m+4��-��-$\frac{1}{4}$m2+$\frac{3}{2}$m+4��=$\frac{1}{4}$m2-2m��
��S=S��CPQ-S��APQ=��m-4��2-16��
��0��S��20��
��A��0��4����B��-2��0����C��8��0����
��AB2+AC2=20+80=100=BC2��
���BAC=90��
����P�͵�B�غ�ʱ��S���=$\frac{1}{2}$��AC��AB=$\frac{1}{2}$��4$\sqrt{5}$��2$\sqrt{5}$=20��
������P�ĺ�����-2��m��0ʱ����P��x���Ϸ�����ֻһ�����㣮
�����á�PAC�����ΪS����Ӧ�ĵ�P����ֻ��2����
���P��������0��m��8ʱ��ֻ����һ����
����ͼ����0��m��8ʱ��ֻ����ͼ��ʾ��λ��ʱ��ֱ��PE��������ֻ��һ������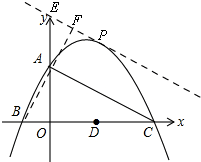
PQ=��-$\frac{1}{4}$m2+$\frac{3}{2}$m+4��-��-$\frac{1}{2}$m+4��=-$\frac{1}{4}$m2+2m��
��S=S��APQ+S��PQC=$\frac{1}{2}$��8����-$\frac{1}{4}$m2+2m��=-��m-4��2+16��
��0��S��16��
�ߵ�P�ĺ�������-2��m��0�������0��S��20��Χ�ڣ���P����������ʼ�մ���һ���㣬
���P�ĺ�������0��m��8�������0��S��16��Χ�ڣ���P��������������ֻ��һ����
��S=16ʱ����Ӧ�ĵ�P����ֻ��������
���� �����Ƕ��κ����ۺ��⣬��Ҫ������Τ�ﶨ����������Ǻ��������������ε����ʺ��ж�������ļ��㣬�Ȿ��Ĺؼ������������Ƶ��ж���



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 1-$\sqrt{2}$ | B�� | -1 | C�� | 1��$\sqrt{2}$ | D�� | 1$��\sqrt{2}$��-1 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
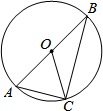 ��ͼ����֪��OΪ��ABC�����Բ����ABΪ��O��ֱ������OC=5��AC=6����BC��Ϊ��������
��ͼ����֪��OΪ��ABC�����Բ����ABΪ��O��ֱ������OC=5��AC=6����BC��Ϊ��������| A�� | 10 | B�� | 9 | C�� | 8 | D�� | ��ȷ�� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com