
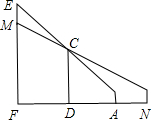
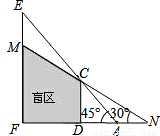
 如图,CD、EF表示高度不同的两座建筑物,小颖站在A处,正好越过前面建筑物的顶端C看到它后面的建筑物的顶端E,仰角为45°;小颖沿直线FA由点A后移10米到达位置点N,正好看到建筑物EF上的点M,仰角为30°.已知小颖的眼睛距离地面1.5米,CD、EF两座建筑物间的距离为25米,求建筑物CD、EF的高(结果保留根号).
如图,CD、EF表示高度不同的两座建筑物,小颖站在A处,正好越过前面建筑物的顶端C看到它后面的建筑物的顶端E,仰角为45°;小颖沿直线FA由点A后移10米到达位置点N,正好看到建筑物EF上的点M,仰角为30°.已知小颖的眼睛距离地面1.5米,CD、EF两座建筑物间的距离为25米,求建筑物CD、EF的高(结果保留根号).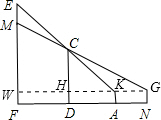
| CH |
| HG |
| x-25 |
| x-15 |
| ||
| 3 |
| 3 |
| 3 |
| 3 |
| 3 |
| 3 |
| 3 |
| 3 |


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
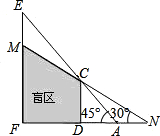 如图,CD,EF表示高度不同的两座建筑物,已知CD高15米,小明站在A处,视线越过CD,能看到它后面的建筑物的顶端E,此时小明的视角∠FAE=45°,为了能看到建筑物EF上点M的位置,小明延直线FA由点A移动到点N的位置,此时小明的视角∠FNM=30°,求AN之间的距离.
如图,CD,EF表示高度不同的两座建筑物,已知CD高15米,小明站在A处,视线越过CD,能看到它后面的建筑物的顶端E,此时小明的视角∠FAE=45°,为了能看到建筑物EF上点M的位置,小明延直线FA由点A移动到点N的位置,此时小明的视角∠FNM=30°,求AN之间的距离.查看答案和解析>>
科目:初中数学 来源: 题型:
 (1)计算:|1-
(1)计算:|1-| 3 |
| 1 |
| 3 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
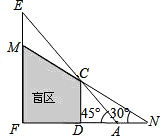 如图,CD,EF表示高度不同的两座建筑物,已知CD高15米,小明站在A处,视线越过CD,能看到它后面的建筑物的顶端E,此时小明的视角∠FAE=45°,为了能看到建筑物EF上点M的位置,小明延直线FA由点A移动到点N的位置,此时小明的视角∠FNM=30°,求AN之间的距离.
如图,CD,EF表示高度不同的两座建筑物,已知CD高15米,小明站在A处,视线越过CD,能看到它后面的建筑物的顶端E,此时小明的视角∠FAE=45°,为了能看到建筑物EF上点M的位置,小明延直线FA由点A移动到点N的位置,此时小明的视角∠FNM=30°,求AN之间的距离.查看答案和解析>>
科目:初中数学 来源:2011年广东省汕尾市海湾中学中考数学专题模拟试卷(四)(解析版) 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com