
【题目】对任意有理数x,用[x]表示不大于x的最大整数.例如:[1.3]=1,[3]=3,[﹣2.5]=﹣3.以下结论正确的是_____.(把你认为正确结论的序号都填上)
①[﹣3.14]=﹣4;
②﹣[﹣x]=[x];
③[2x]=2[x];
④若[![]() ]=﹣4,则x的取值范围是﹣
]=﹣4,则x的取值范围是﹣![]() ≤x<﹣
≤x<﹣![]() .
.
科目:初中数学 来源: 题型:
【题目】我们知道三角形任意两条中线的交点是三角形的重心.重心有如下性质:重心到顶点的距离是重心到对边中点距离的2倍.请利用该性质解决问题

(1)如图1,在△ABC中,AF、BE是中线,AF⊥BE于P.若BP=2,∠FAB=30°,则EP= ,FP= ;
(2)如图1,在△ABC中,BC=a,AC=b,AB=c,AF、BE是中线,AF⊥BE于P.猜想a2、b2、c2三者之间的关系并证明;
(3)如图2,在ABCD中,点E、F、G分别是AD、BC、CD的中点,BE⊥BG,AB=3,AD=2![]() ,求AF的长.
,求AF的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有这样一个问题:探究函数y= ![]() 的图象与性质,小静根据学习函数的经验,对函数y=
的图象与性质,小静根据学习函数的经验,对函数y= ![]() 的图象与性质进行了探究,下面是小静的探究过程,请补充完整:
的图象与性质进行了探究,下面是小静的探究过程,请补充完整: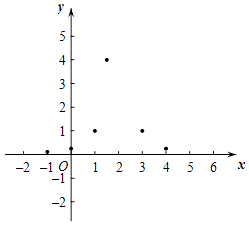
(1)函数y= ![]() 的自变量x的取值范围是;
的自变量x的取值范围是;
(2)下表是y与x的几组对应值.
x | … | ﹣1 | 0 | 1 |
|
| 3 | 4 | … |
y | … |
|
| 1 | 4 | m | 1 |
| … |
表中的m=;
(3)如图,在平面直角坐标系xOy中,描出以上表中各对对应值为坐标的点,根据描出的点画出该函数的图象;
(4)结合函数图象,写出一条该函数图象的性质: .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,已知抛物线与直线的图象如图所示,当y1≠y2时,取y1 , y2中的较大值记为N;当y1=y2时,N=y1=y2 . 则下列说法: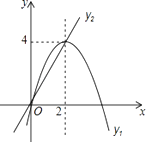
①当0<x<2时,N=y1;
②N随x的增大而增大的取值范围是x<0;
③取y1 , y2中的较小值记为M,则使得M大于4的x值不存在;
④若N=2,则x=2﹣ ![]() 或x=1.
或x=1.
其中正确的有( )
A.1个
B.2个
C.3个
D.4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某中学为丰富学生的校园生活,准备从体育用品商店一次性购买若干个足球和篮球(每个足球的价格相同,每个篮球的价格相同),若购买3个足球和2个篮球共需310元,购买2个足球和5个篮球共需500元。
(1)求购买一个足球、一个篮球各需多少元?
(2)根据学校实际情况,需从体育用品商店一次性购买足球和篮球共96个,要求购买足球和篮球的总费用不超过5720元,这所中学最多可以购买多少个篮球?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我市某中学计划购进若干个甲种规格的排球和乙种规格的足球. 如果购买20个甲种规格的排球和15个乙种规格的足球,一共需要花费2050元; 如果购买10个甲种规格的排球和20个乙种规格的足球,一共需要花费1900元.
(1)求每个甲种规格的排球和每个乙种规格的足球的价格分别是多少元?
(2)如果学校要购买甲种规格的排球和乙种规格的足球共50个,并且预算总费用不超过3210元,那么该学校至多能购买多少个乙种规格的足球?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】经市场调查,某种商品在第x天的售价与销量的相关信息如下表;已知该商品的进价为每件30元,设销售该商品每天的利润为y元.
(1)求出y与x的函数关系式
(2)问销售该商品第几天时,当天销售利润最大?最大利润是多少? .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com