

���� ��1�������A��P��B�����꼴����ã������A��P��B�����꼴����ã�
��2�����ö��κ���ͼ���ϵ��������������P��m��-$\frac{1}{4}$m2-2������B��m��-1����Ȼ����������ľ��빫ʽ�����PA��PB���Ӷ����ж�������ȣ�
��3������Q��0��-1����ֱ��lƽ����x�ᣬ��PB��l��B��DE��l��E����ͼ3���ɣ�1����PB=PA��DE=DA����֤����QDE�ס�QPB���������Ʊȵõ�����DE��PB��������ϵ����P��m��-$\frac{1}{4}$m2-2������B��m��-1����PB=$\frac{1}{4}$m2+1����E������Ϊ��$\frac{1}{4}$m��-1����D������Ϊ[$\frac{1}{4}$m��-$\frac{1}{4}$��$\frac{1}{4}$m��2-2]����ED=$\frac{1}{64}$m2+1��Ȼ�����DE��PB��������ϵ�з���$\frac{1}{4}$m2+1=4��$\frac{1}{64}$m2+1�����ⷽ�����m���Ӷ��õ�P�����꣬������ô���ϵ������ֱ��PQ�Ľ���ʽ��
��� �⣺��1���ٵ�m=0ʱ����P��0��n����
����y=-$\frac{1}{4}$x2-2�ã�n=-2��
��P��0��-2����
��B����Q���غϣ�
�ߵ�A��0��-3������Q��0��-1����
��PA=1��PB=1��
�ڵ�m=2ʱ����P��2��n����
����y=-$\frac{1}{4}$x2-2�ã�n=-3��
��P��2��-3����
�ߵ�A��0��-3������Q��0��-1����
��PA=$\sqrt{{2}^{2}+{0}^{2}}$=2��PB=2��
�ʴ�Ϊ��1��1��2��2��
��2������PA��PB��ȣ��������£�
�������£���P��m��-$\frac{1}{4}$m2-2������B��m��-1����
��PA=$\sqrt{{m}^{2}+��-\frac{1}{4}m-2+3��^{2}}$=$\frac{1}{4}$m2+1��
PB=-1-��-$\frac{1}{4}$m2-2��=$\frac{1}{4}$m2+1��
��PA=PB��
��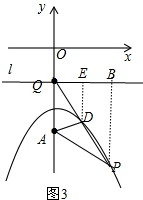 ����Q��0��-1����ֱ��lƽ����x�ᣬ��PB��l��B��DE��l��E����ͼ3���ɣ�1����PB=PA��DE=DA��
����Q��0��-1����ֱ��lƽ����x�ᣬ��PB��l��B��DE��l��E����ͼ3���ɣ�1����PB=PA��DE=DA��
��PA=4AD��
��PB=4DE��
��DE��PB��
���QDE�ס�QPB��
��$\frac{QE}{QB}=\frac{DE}{PB}$=$\frac{1}{4}$��
��P��m��-$\frac{1}{4}$m2-2������B��m��-1����PB=$\frac{1}{4}$m2+1��
��E������Ϊ��$\frac{1}{4}$m��-1����D������Ϊ[$\frac{1}{4}$m��-$\frac{1}{4}$��$\frac{1}{4}$m��2-2]��
��ED=-1+$\frac{1}{4}$��$\frac{1}{4}$m��2+2=$\frac{1}{64}$m2+1��
��$\frac{1}{4}$m2+1=4��$\frac{1}{64}$m2+1�������m1=4��m2=-4��
��P��������4��-6����-4��-6����
��P������Ϊ��4��-6��ʱ��ֱ��PQ�Ľ���ʽΪy=-$\frac{5}{4}$x-1��
��P������Ϊ��-4��-6��ʱ��ֱ��PQ�Ľ���ʽΪy=$\frac{5}{4}$x-1��
��ֱ��PQ�Ľ���ʽΪy=$\frac{5}{4}$x-1��y=-$\frac{5}{4}$x-1��
���� ���⿼���˶��κ������ۺ��⣺�������ն��κ���ͼ���ϵ���������������������ε��ж������ʣ������ô���ϵ������һ�κ�������ʽ������������ͼ�����ʣ���ס�����ľ��빫ʽ�ǽ���Ĺؼ���


 Сѧ���AB��ϵ�д�
Сѧ���AB��ϵ�д� ABC����ȫ�ž�ϵ�д�
ABC����ȫ�ž�ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 1�� | B�� | 2�� | C�� | 3�� | D�� | 4�� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
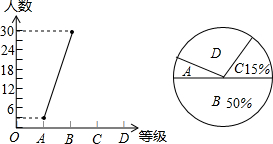 Ϊӭ�ӳ������������д���������ijУ���꼶һ�չ�ˡ����������ļ�ֵ�ۡ�δ�����˻����������ǹ淶����֪ʶ��������ɼ���ΪA��B��C��D�ĸ��ȼ��������ռ������ݻ�����������������ͳ��ͼ���������ͼ������������Ϣ��������и��⣺
Ϊӭ�ӳ������������д���������ijУ���꼶һ�չ�ˡ����������ļ�ֵ�ۡ�δ�����˻����������ǹ淶����֪ʶ��������ɼ���ΪA��B��C��D�ĸ��ȼ��������ռ������ݻ�����������������ͳ��ͼ���������ͼ������������Ϣ��������и��⣺�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
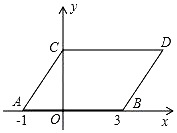 ��ͼ����ƽ��ֱ������ϵ�У���A��B������ֱ�Ϊ��-1��0������3��0������ͬʱ����A��B�ֱ�����ƽ��2����λ��������ƽ��1����λ���ֱ�õ���A��B�Ķ�Ӧ��C��D������AC��BD��CD����ƽ���ı���ABDC
��ͼ����ƽ��ֱ������ϵ�У���A��B������ֱ�Ϊ��-1��0������3��0������ͬʱ����A��B�ֱ�����ƽ��2����λ��������ƽ��1����λ���ֱ�õ���A��B�Ķ�Ӧ��C��D������AC��BD��CD����ƽ���ı���ABDC�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
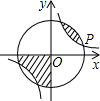 ��ͼ����P��4a��a���Ƿ���������y=$\frac{k}{x}$��k��0�����O��һ�����㣬ͼ����Ӱ���ֵ����Ϊ17�У����������Ľ���ʽΪy=$\frac{16}{x}$��
��ͼ����P��4a��a���Ƿ���������y=$\frac{k}{x}$��k��0�����O��һ�����㣬ͼ����Ӱ���ֵ����Ϊ17�У����������Ľ���ʽΪy=$\frac{16}{x}$���鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com