
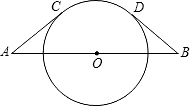
 如图,
如图,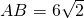 ,O为AB的中点,AC,BD都是半径为3的⊙O的切线,C,D为切点,则
,O为AB的中点,AC,BD都是半径为3的⊙O的切线,C,D为切点,则 的长为
的长为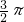
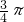

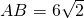 ,O为AB的中点,易求得∠AOC与∠BOD的度数,∠COD的度数,由弧长公式,即可求得
,O为AB的中点,易求得∠AOC与∠BOD的度数,∠COD的度数,由弧长公式,即可求得 的长.
的长.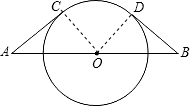 解:连接OC,OD,
解:连接OC,OD, ,O为AB的中点,
,O为AB的中点, ,
, =
= ,
, 的长为:
的长为: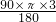 =
= π.
π.

 新课标同步训练系列答案
新课标同步训练系列答案 一线名师口算应用题天天练一本全系列答案
一线名师口算应用题天天练一本全系列答案科目:初中数学 来源: 题型:
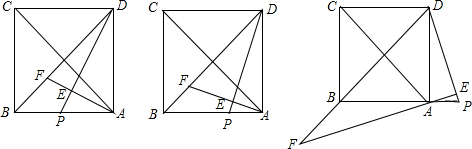
 19、如图,直线CP是AB的中垂线且交AB于P,其中AP=2CP.甲、乙两人想在AB上取两点D、E,使得AD=DC=CE=EB,其作法如下:
19、如图,直线CP是AB的中垂线且交AB于P,其中AP=2CP.甲、乙两人想在AB上取两点D、E,使得AD=DC=CE=EB,其作法如下:查看答案和解析>>
科目:初中数学 来源: 题型:
| BF |
| DF |
| BF |
| AC |
| AP |
| BP |
| 1 |
| 2 |
| BF |
| AC |
| AP |
| AB |
| 1 |
| 3 |
查看答案和解析>>
科目:初中数学 来源: 题型:阅读理解
| 2 |

查看答案和解析>>
科目:初中数学 来源:2012届江苏省沭阳银河学校九年级下学期质量检测数学卷 题型:解答题
如图,在直径为AB的一块半圆形土地上,画出一块三角形区域,使三角形的一边为AB,顶点C在半圆上,其它两边长分别为6cm和8cm,现要建造一个内接于△ABC的矩形水池DEFN,其中DE在AB上,如图所示的设计方案是使AC=8cm,BC=6cm。
(1)求△ABC中AB边上的高h;
(2)设DN=x,当x取何值时,水池DEFN的面积最大?
(3)实际施工时,发现在AB上距B点1.85m处有一棵大树,则这棵大树是否位于最大矩形的边上?如果在,为了保护大树,请你设计出另外的方案,使内接于满足条件的三角形中建最大矩形水池能避开大树。
查看答案和解析>>
科目:初中数学 来源:2011-2012学年江苏省九年级下学期质量检测数学卷 题型:解答题
如图,在直径为AB的一块半圆形土地上,画出一块三角形区域,使三角形的一边为AB,顶点C在半圆上,其它两边长分别为6cm和8cm,现要建造一个内接于△ABC的矩形水池DEFN,其中DE在AB上,如图所示的设计方案是使AC=8cm,BC=6cm。
(1)求△ABC中AB边上的高h;
(2)设DN=x,当x取何值时,水池DEFN的面积最大?
(3)实际施工时,发现在AB上距B点1.85m处有一棵大树,则这棵大树是否位于最大矩形的边上?如果在,为了保护大树,请你设计出另外的方案,使内接于满足条件的三角形中建最大矩形水池能避开大树。

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com