
【题目】已知:二次函数![]() 的图象与x轴交于点A、
的图象与x轴交于点A、![]() ,顶点为
,顶点为![]()
![]() 求该二次函数的解析式;
求该二次函数的解析式;
![]() 如图,过A、C两点作直线,并将线段AC沿该直线向上平移,记点A、C分别平移到点D、E处
如图,过A、C两点作直线,并将线段AC沿该直线向上平移,记点A、C分别平移到点D、E处![]() 若点F在这个二次函数的图象上,且
若点F在这个二次函数的图象上,且![]() 是以EF为斜边的等腰直角三角形,求点F的坐标;
是以EF为斜边的等腰直角三角形,求点F的坐标;
![]() 试确定实数p,q的值,使得当
试确定实数p,q的值,使得当![]() 时,
时,![]() .
.

【答案】(1)该二次函数的解析式为![]() ;(2)点F的坐标为
;(2)点F的坐标为![]() ;(3)满足条件的实数p,q的值为
;(3)满足条件的实数p,q的值为![]() ,
,![]() 或
或![]() ,
,![]() .
.
【解析】分析:(1)由二次函数y=ax2+bx+c的顶点为C(-1,-2),可设其解析式为y=a(x+1)2-2,再把B(-3,0)代入,利用待定系数法即可求出该二次函数的解析式;
(2)由二次函数的解析式求出A(1,0).过点C作CH⊥x轴于点H.解直角△ACH,得出AH=2=CH,那么∠1=45°,AC=2![]() .解等腰直角△DEF得出∠2=45°,EF=4,由∠1=∠2=45°,得到EF∥CH∥y轴.利用待定系数法求出直线AC的解析式为y=x-1.设F(m,
.解等腰直角△DEF得出∠2=45°,EF=4,由∠1=∠2=45°,得到EF∥CH∥y轴.利用待定系数法求出直线AC的解析式为y=x-1.设F(m,![]() m2+m-
m2+m-![]() )(其中m>1),则点E(m,m-1),那么EF=(
)(其中m>1),则点E(m,m-1),那么EF=(![]() m2+m-
m2+m-![]() )-(m-1)=
)-(m-1)=![]() m2-
m2-![]() =4,解方程求出m,进而得出点F的坐标;
=4,解方程求出m,进而得出点F的坐标;
(3)先求出y=![]() 时x1=-4,x2=2.再根据二次函数的性质可知,当p≤x≤q时,p≤y≤
时x1=-4,x2=2.再根据二次函数的性质可知,当p≤x≤q时,p≤y≤![]() ,应分三种情况讨论:①p≤x≤-1;②p<-1≤q;③-1≤p<q.
,应分三种情况讨论:①p≤x≤-1;②p<-1≤q;③-1≤p<q.
详解:![]() 二次函数
二次函数![]() 的顶点为
的顶点为![]() ,
,
![]() 可设该二次函数的解析式为
可设该二次函数的解析式为![]() ,
,
把![]() 代入,得
代入,得![]() ,
,
解得
![]() 该二次函数的解析式为
该二次函数的解析式为![]() ;
;
![]() 由
由![]() ,得
,得![]() 或1,
或1,
![]() .
.
如图,过点C作![]() 轴于点H.
轴于点H.
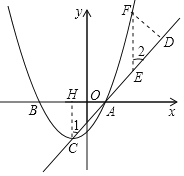
![]() ,
,
![]() ,
,![]() ,
,
又![]() ,
,
![]() ,
,
![]() ,
,![]() .
.
在等腰直角![]() 中,
中,![]() ,
,![]() ,
,
![]() ,
,![]() ,
,
![]() ,
,
![]() 轴.
轴.
由![]() ,
,![]() 可得直线AC的解析式为
可得直线AC的解析式为![]() .
.
由题意,设![]() 其中
其中![]() ,则点
,则点![]() ,
,
![]() ,
,
![]() ,
,![]() 不合题意舍去
不合题意舍去![]() ,
,
![]() 点F的坐标为
点F的坐标为![]() ;
;
![]() 当
当![]() 时,
时,![]() ,解得
,解得![]() ,
,![]() .
.
![]() ,
,
![]() 当
当![]() 时,y随x的增大而减小;当
时,y随x的增大而减小;当![]() 时,y随x的增大而增大;
时,y随x的增大而增大;
当![]() 时,y有最小值
时,y有最小值![]() .
.
![]() 当
当![]() 时,
时,![]() ,
,
![]() 可分三种情况讨论:
可分三种情况讨论:
![]() 当
当![]() 时,由增减性得:
时,由增减性得:
当![]() 时,
时,![]() ,当
,当![]() 时,
时,![]() ,不合题意,舍去;
,不合题意,舍去;
![]() 当
当![]() 时,
时,
![]() Ⅰ
Ⅰ![]() 若
若![]() ,由增减性得:
,由增减性得:
当![]() 时,
时,![]() ,当
,当![]() 时,
时,![]() ,不合题意,舍去;
,不合题意,舍去;
![]() Ⅱ
Ⅱ![]() 若
若![]() ,由增减性得:
,由增减性得:
当![]() 时,
时,![]() ,当
,当![]() 时,
时,![]() ,符合题意,
,符合题意,
![]() ,
,![]() ;
;
![]() 当
当![]() 时,由增减性得:
时,由增减性得:
当![]() 时,
时,![]() ,当
,当![]() 时,
时,![]() ,
,
把![]() ,
,![]() 代入
代入![]() ,得
,得![]() ,
,
解得![]() ,
,![]() 不合题意,舍去
不合题意,舍去![]() ,
,
![]() ,
,![]() .
.
综上所述,满足条件的实数p,q的值为![]() ,
,![]() 或
或![]() ,
,![]() .
.


科目:初中数学 来源: 题型:
【题目】某校计划购进A,B两种树木共100棵进行校园绿化,经市场调查:购买A种树木2棵,B种树木5棵,共需600元;购买A种树木3棵,B种树木1棵,共需380元.
(1)求A,B两种树木每棵各多少元?
(2)因布局需要,购买A种树木的数量不少于B种树木数量的3倍.实际付款总金额按市场价九折优惠,请设计一种购买树木的方案,使实际所花费用最省,并求出最省的费用.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在已有运算的基础上定义一种新运算![]() :
:![]() ,
,![]() 的运算级别高于加减乘除运算,即
的运算级别高于加减乘除运算,即![]() 的运算顺序要优先于
的运算顺序要优先于![]() 运算,试根据条件回答下列问题.
运算,试根据条件回答下列问题.
(1)计算:![]() ;
;
(2)若![]() ,则
,则![]() ;
;
(3)在数轴上,数![]() 的位置如下图所示,试化简:
的位置如下图所示,试化简:![]() ;
;
![]()
(4)如图所示,在数轴上,点![]() 分别以1个单位每秒的速度从表示数-1和3的点开始运动,点
分别以1个单位每秒的速度从表示数-1和3的点开始运动,点![]() 向正方向运动,点
向正方向运动,点![]() 向负方向运动,
向负方向运动,![]() 秒后点
秒后点![]() 分别运动到表示数
分别运动到表示数![]() 和
和![]() 的点所在的位置,当
的点所在的位置,当![]() 时,求
时,求![]() 的值.
的值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读理解:
(探究与发现)
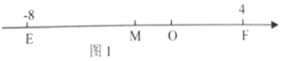
如图1,在数轴上点![]() 表示的数是8,点
表示的数是8,点![]() 表示的数是4,求线段
表示的数是4,求线段![]() 的中点
的中点![]() 所示的数对于求中点表示数的问题,只要用点
所示的数对于求中点表示数的问题,只要用点![]() 所表示的数-8,加上点
所表示的数-8,加上点![]() 所表示的数4,得到的结果再除以2,就可以得到中点
所表示的数4,得到的结果再除以2,就可以得到中点![]() 所表示的数:即
所表示的数:即![]() 点表示的数为:
点表示的数为:![]() .
.
(理解与应用)
把一条数轴在数![]() 处对折,使表示-20和2020两数的点恰好互相重合,则
处对折,使表示-20和2020两数的点恰好互相重合,则![]() .
.
(拓展与延伸)
如图2,已知数轴上有![]() 、
、![]() 、
、![]() 三点,点
三点,点![]() 表示的数是-6,点
表示的数是-6,点![]() 表示的数是8.
表示的数是8.![]() .
.
(1)若点![]() 以每秒3个单位的速度向右运动,点
以每秒3个单位的速度向右运动,点![]() 同时以每秒1个单位的速度向左运动设运动时间为
同时以每秒1个单位的速度向左运动设运动时间为![]() 秒.
秒.
①点![]() 运动
运动![]() 秒后,它在数轴上表示的数表示为 (用含
秒后,它在数轴上表示的数表示为 (用含![]() 的代数式表示)
的代数式表示)
②当点![]() 为线段
为线段![]() 的中点时,求
的中点时,求![]() 的值.
的值.
(2)若(1)中点![]() 、点
、点![]() 的运动速度、运动方向不变,点
的运动速度、运动方向不变,点![]() 从原点以每秒2个单位的速度向右运动,假设
从原点以每秒2个单位的速度向右运动,假设![]() 、
、![]() 、
、![]() 三点同时运动,求多长时间点
三点同时运动,求多长时间点![]() 到点
到点![]() 的距离相等?
的距离相等?

查看答案和解析>>
科目:初中数学 来源: 题型:
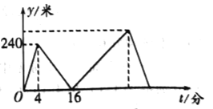
【题目】小莹和小亮在笔直的公路上同起点、同终点、同方向匀速步行![]() 米,先到终点的人原地休息.已知小莹先出发
米,先到终点的人原地休息.已知小莹先出发![]() 分钟,在整个步行过程中,两人的距离
分钟,在整个步行过程中,两人的距离![]() (米)与小莹出发的时间
(米)与小莹出发的时间![]() (分)之间的关系如图所示,下列结论:①小莹的步行速度为
(分)之间的关系如图所示,下列结论:①小莹的步行速度为![]() 米/分;②小亮用
米/分;②小亮用![]() 分钟追上小莹;③小亮走完全程用了
分钟追上小莹;③小亮走完全程用了![]() 分钟;④小亮到达终点时,小莹离终点还有
分钟;④小亮到达终点时,小莹离终点还有![]() 米。其中正确的结论有( )
米。其中正确的结论有( )
A. ![]() 个B.
个B. ![]() 个C.
个C. ![]() 个D.
个D. ![]() 个
个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】现有五张形状、大小、质地都相同的卡片,这些卡片上面分别画有下列图形:①正方形;②等边三角形;③平行四边形;④等腰三角形;⑤圆.将卡片背面朝上洗匀,从中随机抽取一张,抽出的纸片正面图形是轴对称图形,但不是中心对称图形的概率是( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB、CD为⊙O的直径,弦AE∥CD,连接BE交CD于点F,过点E作直线EP与CD的延长线交于点P,使∠PED=∠C.
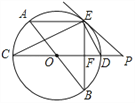
(1)求证:PE是⊙O的切线;
(2)求证:ED平分∠BEP.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲三角形的周长为![]() ,乙三角形的第一条边长为
,乙三角形的第一条边长为![]() ,第二条边长为
,第二条边长为![]() ,第三条边比第二条边短
,第三条边比第二条边短![]() .
.
(1)求乙三角形第三条边的长;
(2)甲三角形和乙三角形的周长哪个大?试说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com