
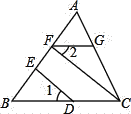
【题目】如图,∠1=∠2,CF⊥AB,DE⊥AB,求证:FG∥BC.
证明:∵CF⊥AB,DE⊥AB (______)
∴∠BED=90°,∠BFC=90° (______)
∴∠BED=∠BFC (______)
∴ED∥FC (______)
∴∠1=∠BCF (______)
∵∠1=∠2 (______)
∴∠2=∠BCF (______)
∴FG∥BC (______)
 期末冲刺100分创新金卷完全试卷系列答案
期末冲刺100分创新金卷完全试卷系列答案科目:初中数学 来源: 题型:
【题目】如图1,在![]() 中,
中,![]() 是角平分线,
是角平分线,![]() 是
是![]() 上的点,
上的点, ![]() 相交于点
相交于点![]() .
.
(1) 如图2,若![]() =90°,求证:
=90°,求证: ![]()
![]() ;
;
(2) 如图1,若![]() =
=![]() ( 0°<
( 0°< ![]() <180°).
<180°).
①求![]()
![]() 的值(用含
的值(用含![]() 的代数式表示);
的代数式表示);
②是否存在![]() ,使
,使![]() 小于
小于![]() ,如果存在,求出
,如果存在,求出![]() 的范围,如果不存在,请说明理由.
的范围,如果不存在,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一定能确定△ABC≌△DEF的条件是( )
A.AB=DE,BC=EF,∠A=∠DB.∠A=∠E,AB=EF,∠B=∠D
C.∠A=∠D,AB=DE,∠B=∠ED.∠A=∠D,∠B=∠E,∠C=∠F
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图:在△ABC中,BE、CF分别是AC、AB两边上的高,在BE上截取BD=AC,在CF的延长线上截取CG=AB,连接AD、AG.
(1)求证:AD=AG;
(2)AD与AG的位置关系如何,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠A=m°,∠ABC和∠ACD的平分线相交于点A1,得∠A1;∠A1BC和∠A1CD的平分线相交于点A2,得∠A2;…;∠A2018BC和∠A2018CD的平分线交于点A2019,则∠A2019=________度.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2019年是大家公认的![]() 商用元年.移动通讯行业人员想了解
商用元年.移动通讯行业人员想了解![]() 手机的使用情况,在某高校随机对500位大学生进行了问卷调查.下列说法正确的是( )
手机的使用情况,在某高校随机对500位大学生进行了问卷调查.下列说法正确的是( )
A.该调查方式是普查
B.该调查中的个体是每一位大学生
C.该调查中的样本是被随机调查的500位大学生![]() 手机的使用情况
手机的使用情况
D.该调査中的样本容量是500位大学生
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,A,B两点在反比例函数y= ![]() 的图象上,C,D两点在反比例函数y=
的图象上,C,D两点在反比例函数y= ![]() 的图象上,AC⊥y轴于点E,BD⊥y轴于点F,AC=2,BD=1,EF=3,则k1﹣k2的值是( )
的图象上,AC⊥y轴于点E,BD⊥y轴于点F,AC=2,BD=1,EF=3,则k1﹣k2的值是( ) 
A.6
B.4
C.3
D.2
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com