
【题目】如图,在△ABC中,AB=AC,D为BC边上一点,且AD=BD,∠ABC=36°.

(1)求∠ADC的度数;
(2)求证:DC=AB.
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】经过某十字路口的汽车,它可能继续直行,也可能向左转或向右转,如果这三种情况是等可能的,当三辆汽车经过这个十字路口时:
(1)求三辆车全部同向而行的概率;
(2)求至少有两辆车向左转的概率;
(3)由于十字路口右拐弯处是通往新建经济开发区的,因此交管部门在汽车行驶高峰时段对车流量作了统计,发现汽车在此十字路口向右转的频率为![]() ,向左转和直行的频率均为
,向左转和直行的频率均为![]() .目前在此路口,汽车左转、右转、直行的绿灯亮的时间分别为30秒,在绿灯亮总时间不变的条件下,为了缓解交通拥挤,请你用统计的知识对此路口三个方向的绿灯亮的时间做出合理的调整.
.目前在此路口,汽车左转、右转、直行的绿灯亮的时间分别为30秒,在绿灯亮总时间不变的条件下,为了缓解交通拥挤,请你用统计的知识对此路口三个方向的绿灯亮的时间做出合理的调整.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读:所谓勾股数就是满足方程![]() 的正整数解,即满足勾股定理的三个正整数构成的一组数
的正整数解,即满足勾股定理的三个正整数构成的一组数![]() 我国古代数学专著
我国古代数学专著![]() 九章算术
九章算术![]() 一书,在世界上第一次给出该方程的解为:
一书,在世界上第一次给出该方程的解为:![]() ,
,![]() ,
,![]() ,其中
,其中![]() ,m,n是互质的奇数.应用:当
,m,n是互质的奇数.应用:当![]() 时,求一边长为8的直角三角形另两边的长.
时,求一边长为8的直角三角形另两边的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,有一正方形广场ABCD,图形中的线段均表示直行道路,![]() 表示一条以A为圆心,以AB为半径的圆弧形道路.如图2,在该广场的A处有一路灯,O是灯泡,夜晚小齐同学沿广场道路散步时,影子长度随行走路线的变化而变化,设他步行的路程为x (m)时,相应影子的长度为y (m),根据他步行的路线得到y与x之间关系的大致图象如图3,则他行走的路线是( )
表示一条以A为圆心,以AB为半径的圆弧形道路.如图2,在该广场的A处有一路灯,O是灯泡,夜晚小齐同学沿广场道路散步时,影子长度随行走路线的变化而变化,设他步行的路程为x (m)时,相应影子的长度为y (m),根据他步行的路线得到y与x之间关系的大致图象如图3,则他行走的路线是( )

A. A→B→E→G B. A→E→D→C C. A→E→B→F D. A→B→D→C
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】数学课上,李老师出示了如下框中的题目.

小敏与同桌小聪讨论后,进行了如下解答:
(1)特殊情况,探索结论:当点E为AB的中点时,如图1,确定线段AE与的DB大小关系.请你直接写出结论:AE DB(填“>”,“<”或“=”).
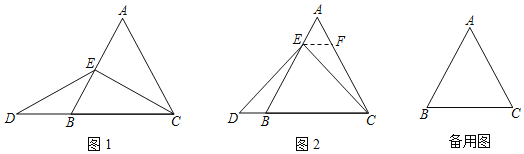
(2)特例启发,解决问题:解:题目中,AE与DB的大小关系是:AE DB(填“>”,“<”或“=”).理由如下:如图2,过点E作EF∥BC,交AC于点F,(请你完成以下解答过程)
(3)拓展结论,设计新题:在等边三角形ABC中,点E在AB的延长线上,点D在直线BC上,且ED=EC.若△ABC的边长为2,AE=3,求CD的长.(请画出符合题意的图形,并直接写出结果)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)如图①②,试研究其中∠1、∠2与∠3、∠4之间的数量关系;

(2)如果我们把∠1、∠2称为四边形的外角,那么请你用文字描述上述的关系式;
(3)用你发现的结论解决下列问题:
如图,AE、DE分别是四边形ABCD的外角∠NAD、∠MDA的平分线,∠B+∠C=240°,求∠E的度数.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,∠AOB=20°,M,N分別是边OA,OB上的定点,P,Q分别是边OB,OA上的动点,记∠OPM=α,∠OQN=β,当MP+PQ+QN最小时,则关于α,β的数量关系正确的是( )

A.β﹣α=30°B.β﹣α=40°C.β+α=180°D.β+α=200°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】本学期学校开展以“感受中华传统美德”为主题的研学活动,组织150名学生参观历史博物馆和民俗展览馆,每一名学生只能参加其中一项活动,共支付票款2000元,票价信息如下:
地点 | 票价 |
历史博物馆 | 10元/人 |
民俗展览馆 | 20元/人 |
(1)请问参观历史博物馆和民俗展览馆的人数各是多少人?
(2)若学生都去参观历史博物馆,则能节省票款多少元?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com