
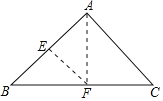
【题目】如图,三角形纸片ABC,AB=AC,∠BAC=90°,点E为AB中点.沿过点E的直线折叠,使点B与点A重合,折痕现交于点F.已知EF=![]() cm, 则BC的长是_______________ .
cm, 则BC的长是_______________ .
 鹰派教辅衔接教材河北教育出版社系列答案
鹰派教辅衔接教材河北教育出版社系列答案 初中暑期衔接系列答案
初中暑期衔接系列答案科目:初中数学 来源: 题型:
【题目】某排球队6名上场队员的身高(单位:![]() )是:180,184,188,190,192,194,现用一名身高为
)是:180,184,188,190,192,194,现用一名身高为![]() 的队员换下场上身高为
的队员换下场上身高为![]() 的队员,与换人前相比,场上队员的身高平均数________.填“变大”.“不变”.“变小”),方差________.(填“变大”.“不变”.“变小”)
的队员,与换人前相比,场上队员的身高平均数________.填“变大”.“不变”.“变小”),方差________.(填“变大”.“不变”.“变小”)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“低碳环保,你我同行”.两年来,扬州市区的公共自行车给市民出行带来切实方便.电视台记者在某区街头随机选取了市民进行调查,调查的问题是“您大概多久使用一次公共自行车?”,将本次调查结果归为四种情况:A.每天都用;B.经常使用;C.偶尔使用;D.从未使用.将这次调查情况整理并绘制如下两幅统计图如图2:

根据图中的信息,解答下列问题:
(1)本次活动共有 位市民参与调查;
(2)补全条形统计图和扇形统计图;
(3)扇形统计图中A项所对应的圆心角的度数为
(4)根据统计结果,若该区有46万市民,请估算每天都用公共自行车的市民约有多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商店需要购进甲、乙两种商品共180件,其进价和售价如表:(注:获利=售价-进价)
甲 | 乙 | |
进价(元/件) | 14 | 35 |
售价(元/件) | 20 | 43 |
(1)若商店计划销售完这批商品后能获利1240元,问甲、乙两种商品应分别购进多少件?
(2)若商店计划投入资金少于5040元,且销售完这批商品后获利多于1312元,请问有哪几种购货方案?并直接写出其中获利最大的购货方案.
查看答案和解析>>
科目:初中数学 来源: 题型:
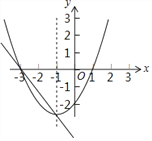
【题目】已知二次函数y1=ax2+bx+c(a≠0)和一次函数y2=kx+n(k≠0)的图象如图所示,下面有四个推断:
①二次函数y1有最大值;
②二次函数y1的图象关于直线x=﹣1对称
③当x=﹣2时,二次函数y1的值大于0
④过动点P(m,0)且垂直于x轴的直线与y1,y2的图象的交点分别为C,D,当点C位于点D上方时,m的取值范围是m<﹣3或m>﹣1.
以上推断正确的是( )
A. ①③ B. ①④ C. ②③ D. ②④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】对任意一个三位数![]() ,如果
,如果![]() 满足各个数位上的数字互不相同,且都不为零,那么称这个数为“相异数”,将一个“相异数”
满足各个数位上的数字互不相同,且都不为零,那么称这个数为“相异数”,将一个“相异数”![]() 的各个数位上的数字之和记为
的各个数位上的数字之和记为![]() . 例如
. 例如![]() 时,
时,![]() .
.
(1)对于“相异数”![]() ,若
,若![]() ,请你写出一个
,请你写出一个![]() 的值;
的值;
(2)若![]() 都是“相异数”,其中
都是“相异数”,其中![]() ,
,![]() (
(![]() ,
,![]() 都是正整数),规定:
都是正整数),规定:![]() ,当
,当![]() 时,求
时,求![]() 的最小值.
的最小值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com