
【题目】将笔记本电脑放置在水平桌面上,显示屏OB与底板OA夹角为115°(如图1),侧面示意图为图2;使用时为了散热,在底板下面垫入散热架O′AC后,电脑转到AO′B′的位置(如图3),侧面示意图为图4,已知OA=0B=20cm,B′O′⊥OA,垂足为C. 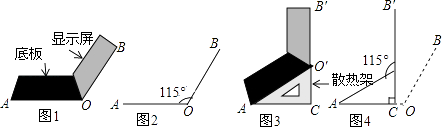
(1)求点O′的高度O′C;(精确到0.1cm)
(2)显示屏的顶部B′比原来升高了多少?(精确到0.1cm)
(3)如图4,要使显示屏O′B′与原来的位置OB平行,显示屏O′B′应绕点O′按顺时针方向旋转多少度? 参考数据:(sin65°=0.906,cos65°=0.423,tan65°=2.146.cot65°=0.446)
【答案】
(1)解:∵B′O′⊥OA,垂足为C,∠AO′B=115°,
∴∠AO′C=65°,
∵cos∠CO′A= ![]() ,
,
∴O′C=O′Acos∠CO′A=20cos65°=8.46≈8.5(cm)
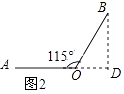
(2)解:如图2,过B作BD⊥AO交AO的延长线于D,
∵∠AOB=115°,
∴∠BOD=65°,
∵sin∠BOD= ![]() ,
,
∴BD=OBsin∠BOD=20×sin65°=18.12,
∴O′B′+O′C﹣BD=20+8.46﹣18.12=10.34≈10.3(cm),
∴显示屏的顶部B′比原来升高了10.3cm
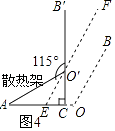
(3)解:如图4,过O′作EF∥OB交AC于E,
∴∠FEA=∠BOA=115°,
∠FOB′=∠EO′C=∠FEA﹣∠O′CA=115°﹣90°=25°,
∴显示屏O′B′应绕点O′按顺时针方向旋转25度
【解析】(1)解直角三角形即可得到结论;(2)如图2,过B作BD⊥AO交AO的延长线于D,根据三角函数的定义即可得到结论;(3)如图4,过O′作EF∥OB交AC于E,根据平行线的性质得到∠FEA=∠BOA=115°,于是得到结论.


科目:初中数学 来源: 题型:
【题目】过双曲线x2﹣ ![]() =1的右支上一点P,分别向圆C1:(x+4)2+y2=4和圆C2:(x﹣4)2+y2=1作切线,切点分别为M,N,则|PM|2﹣|PN|2的最小值为( )
=1的右支上一点P,分别向圆C1:(x+4)2+y2=4和圆C2:(x﹣4)2+y2=1作切线,切点分别为M,N,则|PM|2﹣|PN|2的最小值为( )
A.10
B.13
C.16
D.19
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知四边形ABCD是矩形,cot∠ADB= ![]() ,AB=16.点E在射线BC上,点F在线段BD上,且∠DEF=∠ADB.
,AB=16.点E在射线BC上,点F在线段BD上,且∠DEF=∠ADB.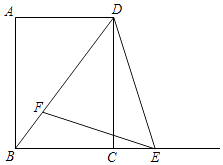
(1)求线段BD的长;
(2)设BE=x,△DEF的面积为y,求y关于x的函数关系式,并写出函数定义域;
(3)当△DEF为等腰三角形时,求线段BE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知在四边形ABCD中,AD∥BC,E为边CB延长线上一点,联结DE交边AB于点F,联结AC交DE于点G,且 ![]() =
= ![]() .
. 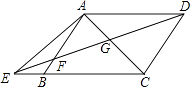
(1)求证:AB∥CD;
(2)如果AD2=DGDE,求证: ![]() =
= ![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形ABCD中,AB=6,AD=3,点P是边AD上的一点,联结BP,将△ABP沿着BP所在直线翻折得到△EBP,点A落在点E处,边BE与边CD相交于点G,如果CG=2DG,那么DP的长是 . 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,矩形ABCD中,M为CD中点,分别以B、M为圆心,以BC长、MC长为半径画弧,两弧相交于点P,若∠PBC=70°,则∠MPC的度数为( ) 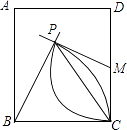
A.55°
B.40°
C.35°
D.20°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系xOy中,一次函数y=k1x+b与反比例函数y= ![]() 的图象交于点A(﹣3,2)和点B(1,m),连接BO并延长与反比例函数y=
的图象交于点A(﹣3,2)和点B(1,m),连接BO并延长与反比例函数y= ![]() 的图象交于点C.
的图象交于点C. 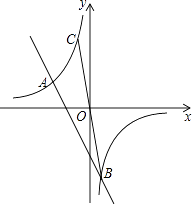
(1)求一次函数y=k1x+b和反比例函数y= ![]() 的表达式;
的表达式;
(2)是否在双曲线y= ![]() 上存在一点D,使得以点A、B、D、C为顶点的四边形成为平行四边形?若存在,请直接写出点D的坐标,并求出该平行四边形的面积;若不存在,请说明理由.
上存在一点D,使得以点A、B、D、C为顶点的四边形成为平行四边形?若存在,请直接写出点D的坐标,并求出该平行四边形的面积;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠ACB=90°,点D,E分别在AB,AC上,CE=BC,连接CD,将线段CD绕点C按顺时针方向旋转90°后得CF,连接EF.
(1)补充完成图形;
(2)若EF∥CD,求证:∠BDC=90°.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com