
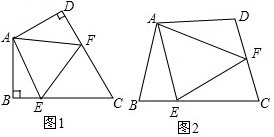
���� ��1���ӳ�FD����G��ʹDG=BE������AG������֤����ABE�ա�ADG���ɵ�AE=AG����֤����AEF�ա�AGF���ɵ�EF=FG�����ɽ��⣻
��2���ӳ�FD����G��ʹDG=BE������AG������֤����ABE�ա�ADG���ɵ�AE=AG����֤����AEF�ա�AGF���ɵ�EF=FG�����ɽ��⣻
��� �⣺��1��EF=BE+DF���������£�
��ͼ���У��ӳ�FD����G��ʹDG=BE������AG��
�ڡ�ABE�͡�ADG�У�
$\left\{\begin{array}{l}{DG=BE}\\{��B=��ADG}\\{AB=AD}\end{array}\right.$��
���ABE�ա�ADG��SAS����
��AE=AG����BAE=��DAG��
�ߡ�EAF=$\frac{1}{2}$��BAD��
���GAF=��DAG+��DAF=��BAE+��DAF=��BAD-��EAF=��EAF��
���EAF=��GAF��
�ڡ�AEF�͡�GAF�У�
$\left\{\begin{array}{l}{AE=AG}\\{��EAF=��GAF}\\{AF=AF}\end{array}\right.$��
���AEF�ա�AGF��SAS����
��EF=FG��
��FG=DG+DF=BE+DF��
��EF=BE+DF��
�ʴ�Ϊ EF=BE+DF��
��2������EF=BE+DF��Ȼ������
���ɣ��ӳ�FD����G��ʹDG=BE������AG����ͼ�ڣ�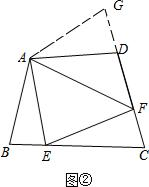
�ڡ�ABE�͡�ADG�У�
$\left\{\begin{array}{l}{DG=BE}\\{��B=��ADG}\\{AB=AD}\end{array}\right.$��
���ABE�ա�ADG��SAS����
��AE=AG����BAE=��DAG��
�ߡ�EAF=$\frac{1}{2}$��BAD��
���GAF=��DAG+��DAF=��BAE+��DAF=��BAD-��EAF=��EAF��
���EAF=��GAF��
�ڡ�AEF�͡�GAF�У�
$\left\{\begin{array}{l}{AE=AG}\\{��EAF=��GAF}\\{AF=AF}\end{array}\right.$��
���AEF�ա�AGF��SAS����
��EF=FG��
��FG=DG+DF=BE+DF��
��EF=BE+DF��
���� ���⿼����ȫ�������ε��ж���������ȫ�������ζ�Ӧ����ȵ����ʣ���������֤��AEF�ա�AGF�ǽ���Ĺؼ���


 ��ս�п�����ϵ�д�
��ս�п�����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
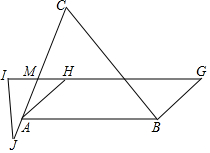 ��ͼ��ʾ����֪HΪ��ABC�Ĵ��ģ���G�����ı���ABGHΪƽ���ı��Σ�IΪֱ��GH�ϵĵ㣬AC��GI��M����IM=MH��JΪCA�ӳ�����һ�㣬��IJ=AH����֤��I��J��G��C�ĵ㹲Բ�������귨���÷֣�
��ͼ��ʾ����֪HΪ��ABC�Ĵ��ģ���G�����ı���ABGHΪƽ���ı��Σ�IΪֱ��GH�ϵĵ㣬AC��GI��M����IM=MH��JΪCA�ӳ�����һ�㣬��IJ=AH����֤��I��J��G��C�ĵ㹲Բ�������귨���÷֣��鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ���Ķ���Ȼ��ش����⣺
���Ķ���Ȼ��ش����⣺�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| x | 0 | 1 | 2 |
| ax2 | 1 | ||
| ax2+bx+c | 5 | 6 |
| A�� | 4.5 | B�� | 9.5 | C�� | -1.5 | D�� | ��ȷ�� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ��1����б���⻭����ȫ������ABCD-A1B1C1D1 ������д��������
��1����б���⻭����ȫ������ABCD-A1B1C1D1 ������д���������鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
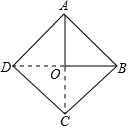 ��ͼ���ֱ��ӳ�����ֱ�ǡ�OAB������ֱ�DZ�AO��BO��ʹAO=OC��BO=OD����֤���ı���ABCD�������Σ�
��ͼ���ֱ��ӳ�����ֱ�ǡ�OAB������ֱ�DZ�AO��BO��ʹAO=OC��BO=OD����֤���ı���ABCD�������Σ��鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
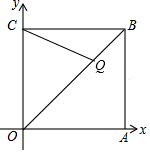 ��ͼ����ƽ��ֱ������ϵ�У��ı���OABC�DZ߳�Ϊ2�������Σ�����A��C�ֱ���x�ᡢy����������ϣ���Q�ڶԽ���OB�ϣ���OQ=OC�����Q������Ϊ��$\sqrt{2}$��$\sqrt{2}$����
��ͼ����ƽ��ֱ������ϵ�У��ı���OABC�DZ߳�Ϊ2�������Σ�����A��C�ֱ���x�ᡢy����������ϣ���Q�ڶԽ���OB�ϣ���OQ=OC�����Q������Ϊ��$\sqrt{2}$��$\sqrt{2}$�����鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
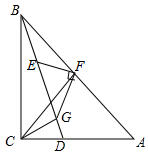 ��ͼ����Rt��ABC�У���ACB=90�㣬AC=BC��D��AC��һ�㣬CG��BD�ڵ�G����E��BD�ϣ���BE=CG����F��AB���е㣬����FE��FG��FC
��ͼ����Rt��ABC�У���ACB=90�㣬AC=BC��D��AC��һ�㣬CG��BD�ڵ�G����E��BD�ϣ���BE=CG����F��AB���е㣬����FE��FG��FC�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com