Question

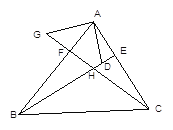
【题目】如图：在△ABC中，BE、CF分别是AC、AB两边上的高，在BE上截取BD=AC，在CF的延长线上截取CG=AB，连结AD、AG。

（1）求证：AD=AG

（2）AD与AG的位置关系如何,请说明理由。

Answer 1

【答案】（1）证明见解析；（2）AD⊥AG，理由见解析

【解析】试题分析：（1）由BE垂直于AC，CF垂直于AB，利用垂直的定义得∠HFB=∠HEC，由得对顶角相等得∠BHF=∠CHE，所以∠ABD=∠ACG．再由AB=CG，BD=AC，利用SAS可得出三角形ABD与三角形ACG全等，由全等三角形的对应边相等可得出AD=AG，（2）利用全等得出∠ADB=∠GAC，再利用三角形的外角和定理得到∠ADB=∠AED+∠DAE，又∠GAC=∠GAD+∠DAE，利用等量代换可得出∠AED=∠GAD=90°，即AG与AD垂直．

试题解析：（1）∵BE⊥AC,CF⊥AB,

∴∠HFB=∠HEC=90°，

又∵∠BHF=∠CHE，

∴∠ABD=∠ACG，

在△ABD和△GCA中

，

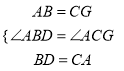∴△ABD≌△GCA(SAS)，

∴AD=GA(全等三角形的对应边相等)；

（2）位置关系是AD⊥GA，

理由为：∵△ABD≌△GCA，

∴∠ADB=∠GAC，

又∵∠ADB=∠AED+∠DAE，∠GAC=∠GAD+∠DAE，

∴∠AED=∠GAD=90°，

∴AD⊥GA.