
| A. | S一定是一个奇数 | B. | S一定是一个偶数 | ||
| C. | S可能是奇数也可能是偶数 | D. | 以上说法都不对 |
 轻松课堂标准练系列答案
轻松课堂标准练系列答案科目:初中数学 来源: 题型:解答题
 实验与探究:三角点阵前n行的点数计算.
实验与探究:三角点阵前n行的点数计算.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
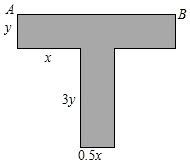 某种T型零件尺寸如图所示(左右宽度相同),求:
某种T型零件尺寸如图所示(左右宽度相同),求:查看答案和解析>>
科目:初中数学 来源: 题型:解答题
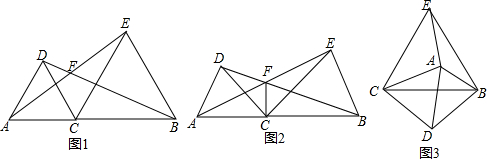
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
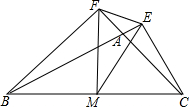 如图,在△ABC中,CE⊥BA的延长线于E,BF⊥CA的延长线于F,M为BC的中点,分别连接ME、MF、EF.
如图,在△ABC中,CE⊥BA的延长线于E,BF⊥CA的延长线于F,M为BC的中点,分别连接ME、MF、EF.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
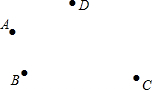 平面上有四个点A、B、C、D,按照以下要求作图:
平面上有四个点A、B、C、D,按照以下要求作图:查看答案和解析>>
科目:初中数学 来源: 题型:解答题
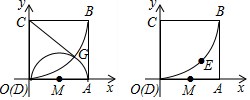 如图,正方形ABCD的顶点A,C分别在x轴,y轴正半轴上,点B的坐标为(10,10),以点C为圆心,CB为半径画弧OB.
如图,正方形ABCD的顶点A,C分别在x轴,y轴正半轴上,点B的坐标为(10,10),以点C为圆心,CB为半径画弧OB.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com