
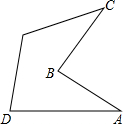
 某地铁站口的垂直截图如图所示,已知∠A=30°,∠ABC=75°,AB=BC=4米,求C点到地面AD的距离(结果保留根号).
某地铁站口的垂直截图如图所示,已知∠A=30°,∠ABC=75°,AB=BC=4米,求C点到地面AD的距离(结果保留根号). 科目:初中数学 来源: 题型:解答题
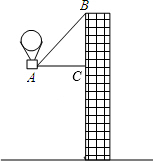 如图,有一热气球到达A处时,仪器显示其正前方一高楼顶部B的仰角是43°,与楼的水平距离AC为12米,为了安全飞越高楼,气球应至少再上升多少米?(结果精确到0.1米)
如图,有一热气球到达A处时,仪器显示其正前方一高楼顶部B的仰角是43°,与楼的水平距离AC为12米,为了安全飞越高楼,气球应至少再上升多少米?(结果精确到0.1米)查看答案和解析>>
科目:初中数学 来源: 题型:填空题
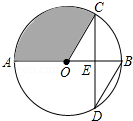 如图,AB是⊙O的直径,弦CD交AB于点E,且E为OB的中点,∠CDB=30°,CD=4$\sqrt{3}$,则阴影部分的面积$\frac{16}{3}$π.
如图,AB是⊙O的直径,弦CD交AB于点E,且E为OB的中点,∠CDB=30°,CD=4$\sqrt{3}$,则阴影部分的面积$\frac{16}{3}$π.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
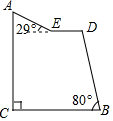 “蘑菇石”是我国著名的自然保护区梵净山的标志,小明从山脚B点先乘坐缆车到达观景平台DE观景,然后再沿着坡脚为29°的斜坡由E点步行到达“蘑菇石”A点,“蘑菇石”A点到水平面BC的垂直距离为1890m.如图,DE∥BC,BD=1800m,∠DBC=80°,求斜坡AE的长度.(结果精确到0.1m,可参考数据sin29°≈0.4848,sin80°≈0.9848,cos29°≈0.8746,cos80°≈0.1736)
“蘑菇石”是我国著名的自然保护区梵净山的标志,小明从山脚B点先乘坐缆车到达观景平台DE观景,然后再沿着坡脚为29°的斜坡由E点步行到达“蘑菇石”A点,“蘑菇石”A点到水平面BC的垂直距离为1890m.如图,DE∥BC,BD=1800m,∠DBC=80°,求斜坡AE的长度.(结果精确到0.1m,可参考数据sin29°≈0.4848,sin80°≈0.9848,cos29°≈0.8746,cos80°≈0.1736)查看答案和解析>>
科目:初中数学 来源: 题型:解答题
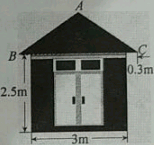 一个住宅区的配电房示意图如图所示,它是一个轴对称图形.已知∠ABC=35°,求配电房房顶离地面的高度(精确到0.1m).(参考数据:sin35°≈0.57,cos35°≈0.82,tan35°≈0.70)
一个住宅区的配电房示意图如图所示,它是一个轴对称图形.已知∠ABC=35°,求配电房房顶离地面的高度(精确到0.1m).(参考数据:sin35°≈0.57,cos35°≈0.82,tan35°≈0.70)查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com