
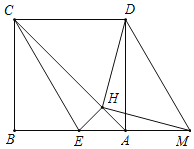
【题目】如图,已知正方形ABCD,点M是边BA延长线上的动点(不与点A重合),且AM<AB,△CBE由△DAM平移得到.若过点E作EH⊥AC,H为垂足,则有以下结论:
①点M位置变化,使得∠DHC=60°时,2BE=DM;
②无论点M运动到何处,都有DM=![]() HM;
HM;
③无论点M运动到何处,∠CHM一定大于135°.其中正确结论的序号为( )
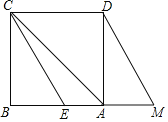
A.①③B.①②C.②③D.①②③
【答案】D
【解析】
根据正方形的性质可证得△MEH≌△DAH,再得到△DHM是等腰直角三角形,故DM=![]() HM,②正确;当∠DHC=60°时,可求得∠ADM=45°﹣15°=30°,故Rt△ADM中,DM=2AM,DM=2BE,①正确;再根据点M是边BA延长线上的动点(不与点A重合),且AM<AB,∠AHM<∠BAC=45°,即可判断.
HM,②正确;当∠DHC=60°时,可求得∠ADM=45°﹣15°=30°,故Rt△ADM中,DM=2AM,DM=2BE,①正确;再根据点M是边BA延长线上的动点(不与点A重合),且AM<AB,∠AHM<∠BAC=45°,即可判断.
由题可得,AM=BE,
∴AB=EM=AD,
∵四边形ABCD是正方形,EH⊥AC,
∴EM=AD,∠AHE=90°,∠MEH=∠DAH=45°=∠EAH,
∴EH=AH,
∴△MEH≌△DAH(SAS),
∴∠MHE=∠DHA,MH=DH,
∴∠MHD=∠AHE=90°,△DHM是等腰直角三角形,
∴DM=![]() HM,故②正确;
HM,故②正确;
当∠DHC=60°时,∠ADH=60°﹣45°=15°,
∴∠ADM=45°﹣15°=30°,
∴Rt△ADM中,DM=2AM,
即DM=2BE,故①正确;
∵点M是边BA延长线上的动点(不与点A重合),且AM<AB,
∴∠AHM<∠BAC=45°,
∴∠CHM>135°,故③正确;
由上可得正确结论的序号为①②③.
故选:D.


 轻巧夺冠周测月考直通中考系列答案
轻巧夺冠周测月考直通中考系列答案科目:初中数学 来源: 题型:
【题目】儿童节前,某玩具商店根据市场调查,用3000元购进一批儿童玩具,上市后很快脱销,接着又用5400元购进第二批这种玩具,所购数量是第一批数量的1.5倍,但每套进价多了10元.
(1)求第一批玩具每套的进价是多少元?
(2)如果这两批玩具每套售价相同,且全部售完后总利润不低于25%,那么每套玩具售价至少是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
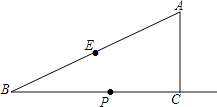
【题目】如图,在Rt△ABC中,∠ACB=90°,∠B=30°,AC=2,E为斜边AB的中点,点P是射线BC上的一个动点,连接AP、PE,将△AEP沿着边PE折叠,折叠后得到△EPA′,当折叠后△EPA′与△BEP的重叠部分的面积恰好为△ABP面积的四分之一,则此时BP的长为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某市甲、乙、丙三个景区是人们节假日游玩的热点景区,某学校对九(5)班学生“五一”小长假随父母到这三个景区游玩的计划做了全面调查,调查分四个类别A:游三个景区:B:游两个景区;C:游一个景区:D:不到这三个景区游玩,现根据调查结果绘制了不完全的条形统计图和扇形统计图如下:
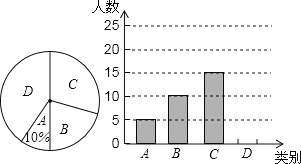
请结合图中信息解答下列问题:
(1)九(5)班现有学生人,并补全条形统计图;
(2)求在扇形统计图中表示“B类别”的扇形的圆心角的度数;
(3)根据调查显示,小刘和小何都选择“C类别”,求他俩游玩的恰好是同一景区的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
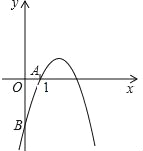
【题目】如图,抛物线y=﹣x2+5x+n经过点A(1,0),与y轴交于点B.
(1)求抛物线的解析式;
(2)P是y轴正半轴上一点,且△PAB是以AB为腰的等腰三角形,试求P点坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
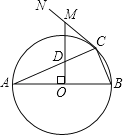
【题目】如图,AB是⊙O的直径,点C为⊙O上一点,CN为⊙O的切线,OM⊥AB于点O,分别交AC、CN于D、M两点.
(1)求证:MD=MC;
(2)若⊙O的半径为5,AC=4![]() ,求MC的长.
,求MC的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了践行“金山银山,不如绿水青山”的环保理念,重外环保小组的孩子们参与社区公益活动——收集废旧电池,活动开展一个月后,经过统计发现,全组成员平均每人收集了![]() 颗废旧电池,其中,收集数量低于
颗废旧电池,其中,收集数量低于![]() 颗的同学平均每人收集了
颗的同学平均每人收集了![]() 颗,收集数量不低于
颗,收集数量不低于![]() 颗的同学平均每人收集了
颗的同学平均每人收集了![]() 颗,数学王老师发现,若每人再多收集
颗,数学王老师发现,若每人再多收集![]() 颗,则收集数量低于
颗,则收集数量低于![]() 颗的同学平均每人收集了
颗的同学平均每人收集了![]() 颗,收集数量不低于
颗,收集数量不低于![]() 颗的同学平均每人收集了
颗的同学平均每人收集了![]() 颗,并且,该环保小组的人数介于
颗,并且,该环保小组的人数介于![]() 至
至![]() 人.则该环保小组有__________人.
人.则该环保小组有__________人.
查看答案和解析>>
科目:初中数学 来源: 题型:
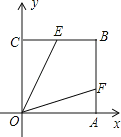
【题目】如图,在正方形OABC中,点B的坐标是(4,4),点E、F分别在边BC、BA上,OE=2![]() .若∠EOF=45°,则F点的纵坐标是( )
.若∠EOF=45°,则F点的纵坐标是( )
A.1B.![]() C.
C.![]() D.
D.![]() ﹣1
﹣1
查看答案和解析>>
科目:初中数学 来源: 题型:
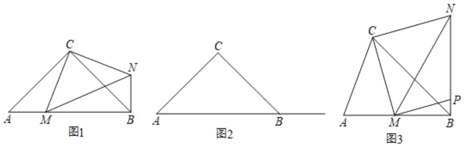
【题目】在△ABC中,∠ABC为锐角,点M为射线AB上一动点,连接CM,以点C为直角顶点,以CM为直角边在CM右侧作等腰直角三角形CMN,连接NB.
(1)如图1,图2,若△ABC为等腰直角三角形,
问题初现:①当点M为线段AB上不与点A重合的一个动点,则线段BN,AM之间的位置关系是 ,数量关系是 ;
深入探究:②当点M在线段AB的延长线上时,判断线段BN,AM之间的位置关系和数量关系,并说明理由;
(2)如图3,∠ACB≠90°,若当点M为线段AB上不与点A重合的一个动点,MP⊥CM交线段BN于点P,且∠CBA=45°,BC=![]() ,当BM= 时,BP的最大值为 .
,当BM= 时,BP的最大值为 .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com