Question

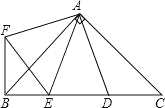
【题目】如图，在Rt△ABC中，AB=AC，D，E是斜边上BC上两点，且∠DAE=45°，将△ADC绕点A顺时针旋转90°后，得到△AFB，连接EF，下列结论：

①BF⊥BC；②△AED≌△AEF；③BE+DC=DE；④BE2+DC2=DE2

其中正确的个数是（ ）

A．1 B．2 C．3 D．4

Answer 1

【答案】C．

【解析】

试题分析：∵△ADC绕点A顺时针旋转90°后，得到△AFB，∴△ADC≌△AFB，∴BF=DC，∠FBA=∠C∠BAF=∠CAD，又∵∠ABC+∠C=90°，∴∠ABC+∠FBA=90°，即∠FBC=90°，∴BF⊥BC，故①正确；

∵∠BAC=90°，∠DAE=45°，∴∠BAE+∠CAD=∠DAE=45°，∴∠BAE+∠BAF=∠DAE=45°，即∠EAF=∠EAD，在△AED和△AEF中，AF=AD,∠EAF=∠EAD,AE=AE，∴△AED≌△AEF，故②正确；

∵BF=DC，∴BE+DC=BE+BF，∵△AED≌△AEF，∴EF=DE，在△BEF中，∵BE+BF＞EF，∴BE+DC＞DE，故③错误；

∵∠FBC=90°，∴BE2+BF2=EF2，∵BF=DC、EF=DE，∴BE2+DC2=DE2，④正确；故选C．