
分析 先把除法运算化为乘法运算,再把a-b利用因式分解的方法变形后约分,然后进行二次根式的乘法法则运算.
解答 解:原式=$\sqrt{ab}$•$\frac{a-b}{\sqrt{a}+\sqrt{b}}$
=$\sqrt{ab}$•$\frac{(\sqrt{a}+\sqrt{b})(\sqrt{a}-\sqrt{b})}{\sqrt{a}+\sqrt{b}}$
=$\sqrt{ab}$($\sqrt{a}$-$\sqrt{b}$)
=a$\sqrt{b}$-b$\sqrt{a}$.
点评 本题考查了二次根式的混合运算:先把各二次根式化简为最简二次根式,然后进行二次根式的乘除运算,再合并即可.


科目:初中数学 来源: 题型:选择题
 如图,在四边形ABCD的外侧,以四边形的边为边分别作四个小正方形,连接相邻的两个顶点,得到四个阴影三角形,则这四个阴影三角形的面积a、b、c、d满足( )
如图,在四边形ABCD的外侧,以四边形的边为边分别作四个小正方形,连接相邻的两个顶点,得到四个阴影三角形,则这四个阴影三角形的面积a、b、c、d满足( )| A. | a+b=c+d | B. | a2+b2=c2+d2 | C. | a+c=b+d | D. | a2+c2=b2+d2 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
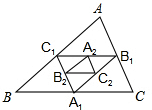 如图,在△ABC中,A1、B1、C1分别是BC、CA、AB的中点,A2、B2、C2分别是B1C1、C1A1、A1B1的中点,…,An、Bn、Cn分别是Bn-1Cn-1、Cn-1An-1、An-1Bn-1的中点,假设△ABC的周长为a,则△A1B1C1的周长为$\frac{1}{2}$a,△A2B2C2的周长为$\frac{1}{4}$a,…,△AnBnCn的周长为$\frac{1}{{2}^{n}}$a.
如图,在△ABC中,A1、B1、C1分别是BC、CA、AB的中点,A2、B2、C2分别是B1C1、C1A1、A1B1的中点,…,An、Bn、Cn分别是Bn-1Cn-1、Cn-1An-1、An-1Bn-1的中点,假设△ABC的周长为a,则△A1B1C1的周长为$\frac{1}{2}$a,△A2B2C2的周长为$\frac{1}{4}$a,…,△AnBnCn的周长为$\frac{1}{{2}^{n}}$a.查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
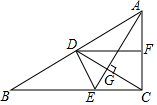 如图,在△ABC中,∠ACB=90°,AE平分∠BAC,CD⊥AE交AE于点G,交AB于点D,DF∥BE交AC于点F.求证:DC平分∠FDE.
如图,在△ABC中,∠ACB=90°,AE平分∠BAC,CD⊥AE交AE于点G,交AB于点D,DF∥BE交AC于点F.求证:DC平分∠FDE.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,在△ABC中,点D、E分别在边AB、AC上,DE∥BC,$\frac{AD}{BD}$=$\frac{1}{2}$,$\overrightarrow{DA}$=$\overrightarrow{a}$,$\overrightarrow{DC}$=$\overrightarrow{b}$
如图,在△ABC中,点D、E分别在边AB、AC上,DE∥BC,$\frac{AD}{BD}$=$\frac{1}{2}$,$\overrightarrow{DA}$=$\overrightarrow{a}$,$\overrightarrow{DC}$=$\overrightarrow{b}$查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com