
| A. | ((13-x)=20 | B. | x($\frac{13-x}{2}$)=20 | C. | x(13-$\frac{1}{2}$x)=20 | D. | x($\frac{13-2x}{2}$)=20 |
科目:初中数学 来源: 题型:选择题
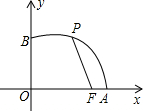 如图,已知点F的坐标为(3,0),点A、B分别是某函数图象与x轴、y轴的交点,点P是此图象上的一动点,设点P的横坐标为x,PF的长为d,且d与x之间满足关系:d=5-$\frac{3}{5}$x(0≤x≤5),则结论:①AF=2;②BF=4;③OA=5;④OB=3,正确结论的序号是( )
如图,已知点F的坐标为(3,0),点A、B分别是某函数图象与x轴、y轴的交点,点P是此图象上的一动点,设点P的横坐标为x,PF的长为d,且d与x之间满足关系:d=5-$\frac{3}{5}$x(0≤x≤5),则结论:①AF=2;②BF=4;③OA=5;④OB=3,正确结论的序号是( )| A. | ①②③ | B. | ①③ | C. | ①②④ | D. | ③④ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | ①④ | B. | ③④ | C. | ②③ | D. | ④⑤ |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
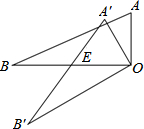 如图,△AOB中,∠AOB=90°,AO=3,BO=6,△AOB绕顶点O逆时针旋转到△AOB处,此时线段A′B′与BO的交点E为BO的中点,则线段B′E的长度为$\frac{9\sqrt{5}}{5}$.
如图,△AOB中,∠AOB=90°,AO=3,BO=6,△AOB绕顶点O逆时针旋转到△AOB处,此时线段A′B′与BO的交点E为BO的中点,则线段B′E的长度为$\frac{9\sqrt{5}}{5}$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\left\{\begin{array}{l}{2x+3y=4}\\{2x+3=4(z+1)}\end{array}\right.$ | B. | $\left\{\begin{array}{l}{\frac{10}{x}+3y=17}\\{8x-3y=1}\end{array}\right.$ | ||
| C. | $\left\{\begin{array}{l}{\frac{m}{2}=1}\\{2m+n=16}\end{array}\right.$ | D. | $\left\{\begin{array}{l}{\frac{x+2y}{z}=1}\\{\frac{2x-y}{3}=1}\end{array}\right.$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com